Circumference is a geometric figure with a circular shape that is part of analytic geometry studies. Note that all points on a circle are equidistant from its radius (r).
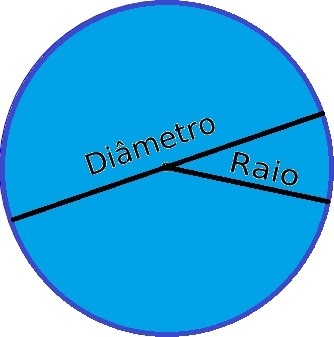
Radius and Diameter of Circumference
Remember that the radius of the circle is a segment that connects the center of the figure to any point located at its end.
The diameter of the circle is a straight line that passes through the center of the figure, dividing it into two equal halves. Therefore, the diameter equals twice the radius (2r).
Reduced Circumference Equation
The reduced equation of the circle is used to determine the different points of a circle, thus helping in its construction. It is represented by the following expression:
(x - a)2 + (y - b)2 = r2
Where the coordinates of A are the points (x, y) and of C are the points (a, b).
General Equation of Circumference
The general equation of the circumference is given from the development of the reduced equation.
x2 + y2 – 2 ax – 2by + a2 + b2 – r2 = 0
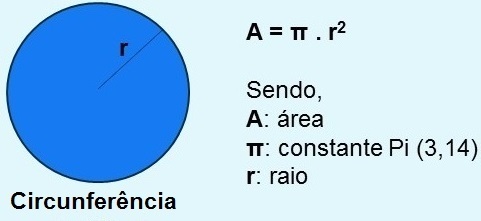
Circumference Area
The area of a figure determines the size of that figure's surface. In the case of the circle, the area formula is:
Want to know more? Also read the article: Flat Figure Areas.
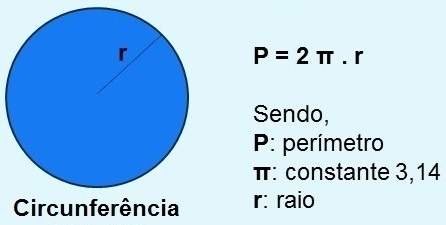
Circumference Perimeter
The perimeter of a flat figure corresponds to the sum of all sides of that one figure.
In the case of the circumference, the perimeter is the size of the measure of the figure's outline, being represented by the expression:
Complement your knowledge by reading the article: Perimeters of Flat Figures.
Length of Circumference
The length of the circumference is closely related to its perimeter. Thus, the greater the radius of this figure, the greater its length.
To calculate the length of a circle we use the same formula as the perimeter:
C = 2 π. r
from where,
C: length
π: constant Pi (3.14)
r: lightning
Circumference and Circle
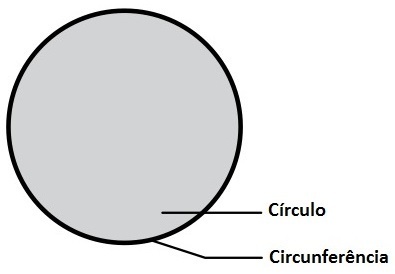
Very common there is confusion between the circumference and the circle. Although we use these terms synonymously, they differ.
While the circumference represents the curved line that limits the circle (or disk), this is a figure limited by the circumference, that is, it represents its internal area.
Learn more about the circle by reading the articles:
- Circle Area
- Circle Perimeter
- Area and Perimeter
Solved Exercises
1. Calculate the area of a circle that has a radius of 6 meters. Consider π = 3.14
A = π. r2
A = 3.14. (6)2
A = 3.14. 36
A = 113.04 m2
2. What is the perimeter of a circle whose radius is 10 meters? Consider π = 3.14
P = 2 π. r
P = 2 π. 10
P = 2. 3,14 .10
P = 62.8 meters
3. If a circle has a radius of 3.5 meters, what will its diameter be?
a) 5 meters
b) 6 meters
c) 7 meters
d) 8 meters
e) 9 meters
Alternative c, as the diameter equals twice the measure of the radius of the circle.
4. What is the radius value of a circle whose area is equal to 379.94 m2? Consider π = 3.14
Using the area formula, we can find the radius value of this figure:
A = π. r2
379,94 = π. r2
379,94 = 3,14. r2
r2 = 379,94/3,14
r2 = 121
r = √ 121
r = 11 meters
5. Find the general equation of the circle whose center has the coordinates C (2, –3) and radius r = 4.
First, we must pay attention to the reduced equation of this circumference:
(x – 2)2 + (y + 3)2 = 16
Once that's done, let's develop the reduced equation to find the general equation for this circle:
x2 – 4x + 4 + y2 + 6y + 9 - 16 = 0
x2 + y2 – 4x + 6y – 3 = 0