Simple and weighted arithmetic average exercises (with template)

THE average aritmetics it is a measure of central tendency, used to summarize a set of data.

There are two main types of media: a simple average and the weighted average. To learn about these two types of media, read our article on arithmetic average.

ANDxercises - Simple arithmetic mean and weighted arithmetic mean

1) Calculate the mean of the following values: 2, 5, 7, 7, 4, 10, 11, 11 and 15.

2) The grades of a class of students on the biology test were 10, 9, 9, 8, 7, 7, 7, 6, 4 and 2. What is the class average?

3) The biology teacher gave another chance to the two students who had grades below 6. These students took a new test and the grades were 7 and 6.5. Calculate the new class average and compare with the average obtained in the previous exercise.

4) The average age of the five players on a basketball team is 25 years. If the pivot of this team, which is 27 years old, is replaced by a 21-year-old player and the other players are kept, then the average age of this team, in years, will become how much?

instagram story viewer

5) The average between 80 values is equal to 52. Of these 80 values, three are removed, 15, 79, 93. What is the average of the remaining values?

6) Determine the weighted average of the numbers 16, 34 and 47 with weights 2, 3 and 6, respectively.

7) If in a purchase, two notebooks cost R$8.00 each and three notebooks cost R$20.00 each. What is the average price of purchased notebooks?

8) In an English course, weights were assigned to the activities: test 1 with weight 2, test 2 with weight 3 and work with weight 1. If Marina got a grade of 7.0 in test 1, grade 6.0 in test 2 and 10.0 in her work, what is the average of Marina's grades?

9) A cake factory sold 250 cakes at R$9.00 each and 160 cakes at R$7.00 each. On average, how much was each of the cakes sold for?

10) A school held a competition to see how many words each of the 50 students could spell correctly. The table below shows the number of correctly spelled words and their respective frequencies. What is the average number of words that students got right? Frequency table

Index

Resolution of exercise 1
Resolution of exercise 2
Resolution of exercise 3
Resolution of exercise 4
Resolution of exercise 5
Resolution of exercise 6
Resolution of exercise 7
Resolution of exercise 8
Resolution of exercise 9
Resolution of exercise 10

Resolution of exercise 1

Let's calculate the simple arithmetic mean ( $\dpi{120} \overline{x}_s$ ) of the values:

$\dpi{120} \overline{x}_s= \frac{2+ 5+ 7+ 7+ 4+ 10+ 11+ 11+ 15}{9}$

$\dpi{120} \overline{x}_s= \frac{72}{9}$

$\dpi{120} \overline{x}_s=8$

Thus, the mean of the values is equal to 8.

Resolution of exercise 2

The average of the grades is given by:

$\dpi{120} \overline{x}_s= \frac{10+ 9+ 9+ 8+ 7+ 7+ 7+ 6+ 4 +2}{10}$

$\dpi{120} \overline{x}_s= \frac{69}{10}$

$\dpi{120} \overline{x}_s= 6.9$

Therefore, the average of the grades of the class is equal to 6.9.

Resolution of exercise 3

The new class average is given by:

$\dpi{120} \overline{x}_s= \frac{10+ 9+ 9+ 8+ 7+ 7+ 7+ 6+ 7 + 6.5}{10}$

$\dpi{120} \overline{x}_s= \frac{76.5}{10}$

$\dpi{120} \overline{x}_s= 7.65$

Thus, the average of the class becomes 7.65. We can observe that the substitution for two higher grades generated an increase in the class average.

Resolution of exercise 4

The average age of the five players is given by:

$\dpi{120} \overline{x}_s= \frac{x_1+x_2+x_3+x_4+x_5}{5}=25$

On what $\dpi{120} x_1,x_2,x_3,x_4 \ \textnormal{e} \ x_5$ are the ages of the five players.

Multiplying cross, we get:

$\dpi{120} x_1+x_2+x_3+x_4+x_5=25\cdot 5$

Then:

$\dpi{120} x_1+x_2+x_3+x_4+x_5=125$

Which means that the sum of the ages of the five players equals 125.

Included in this calculation is the player's age of 27. As he will turn out, we must subtract his age:

$\dpi{120} 125 - 27 = 98$ To the result we will add the age of the player who will join, who is 21 years old:

$\dpi{120} 98 + 21 = 119$

Thus, the sum of the ages of the five players on the team, with the substitution, will be 119 years old.

Dividing this number by 5, we get the new average:

$\dpi{120} \overline{x}_s=\frac{119}{5} = 23.8.$

Therefore, the average age of the team, with the replacement, will be 23.8 years.

Resolution of exercise 5

The average of the 80 values is given by:

$\dpi{120} \overline{x}_s= \frac{x_1+x_2+...+x_{80}}{80}=52$

On what $\dpi{120} x_1,x_2,..., x_{80}$ are the 80 values.

Multiplying cross, we get:

$\dpi{120} x_1+x_2+...+x_{80}=52\cdot 80$

Then:

$\dpi{120} x_1+x_2+...+x_{80}=4160$

Which means the sum of the 80 values equals 4160.

As the values 15, 79 and 93 will be removed, we must subtract them from this total:

$\dpi{120} 4160 - 15-79-93 = 3973$

It means that the sum of the remaining 77 values is equal to 3973.

Dividing this number by 77, we get the new average:

$\dpi{120} \overline{x}_s= \frac{3973}{77}\approx 51.59$

Thus, the average of the remaining values is approximately equal to 51.59.

Check out some free courses

Free Online Inclusive Education Course
Free Online Toy Library and Learning Course
Free Online Math Games Course in Early Childhood Education
Free Online Pedagogical Cultural Workshops Course

Resolution of exercise 6

The weighted average ( $\dpi{120} \overline{x}_p$ ) of these values is given by:

$\dpi{120} \overline{x}_p=\frac{16\cdot 2+34\cdot 3+47\cdot 6}{11}$

$\dpi{120} \overline{x}_p=\frac{32+102+282}{11}$

$\dpi{120} \overline{x}_p=\frac{416}{11}$

$\dpi{120} \overline{x}_p\approx 37.81$

So the weighted average of these three numbers is approximately equal to 37.81.

Resolution of exercise 7

This exercise can be solved by simple average and weighted average.

By simple average:

Let's add up the price of all notebooks and divide by the amount of notebooks purchased.

$\dpi{120} \overline{x}_s= \frac{8 + 8+20+20+20}{5}$

$\dpi{120} \overline{x}_s= \frac{76}{5}$

$\dpi{120} \overline{x}_s= 15.2$

The notebooks cost an average of R$15.20.

By weighted average:

We want to get average prices. So the notebook quantities are the weights, whose sum is 5.

$\dpi{120} \overline{x}_p=\frac{8\cdot 2+20\cdot 3}{5}$

$\dpi{120} \overline{x}_p=\frac{76}{5}$

$\dpi{120} \overline{x}_p= 15.2$

As expected, we get the same value for the average price of notebooks.

Resolution of exercise 8

Let's calculate the weighted average of the grades by their respective weights:

$\dpi{120} \overline{x}_p=\frac{7.0\cdot 2+6.0\cdot 3+10.0\cdot 1}{6}$

$\dpi{120} \overline{x}_p=\frac{14.0+18.0+10.0}{6}$

$\dpi{120} \overline{x}_p=\frac{42.0}{6}$

$\dpi{120} \overline{x}_p =7.0$

Thus, Marina's average grade is 7.0.

Resolution of exercise 9

The average price of cakes is given by:

$\dpi{120} \overline{x}_p=\frac{9\cdot 250+7\cdot 160}{410}$

$\dpi{120} \overline{x}_p=\frac{2250+1120}{410}$

$\dpi{120} \overline{x}_p=\frac{3370}{410}$

$\dpi{120} \overline{x}_p\approx 8.21$

Soon, the cakes were sold, on average, for R$8.21 each.

Resolution of exercise 10

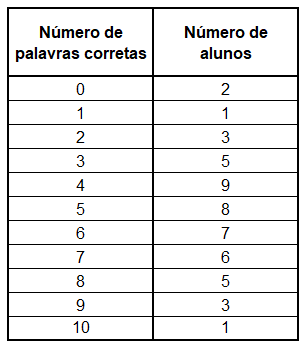
The average amount of correctly spelled words is given by:

$\dpi{120} \overline{x}_p=\frac{0\cdot 2+1\cdot 1+2\cdot 3+3\cdot 5+4\cdot 9+5\cdot 8+6\cdot 7+ 7\cdot 6+8\cdot 5+9\cdot 3+10\cdot 1}{50}$

$\dpi{120} \overline{x}_p=\frac{0+1+6+15+36+40+42+42+40+27+10}{50}$

$\dpi{120} \overline{x}_p=\frac{259}{50}$

$\dpi{120} \overline{x}_p=5.18$

So, the average number of words spelled correctly by the students was 5.18 words.

See too: Trigonometric Functions - Sine, Cosine and Tangent

The password has been sent to your email.