Exercises on orthogonal projections

Check out a list of solved exercises on orthogonal projections and learn more about this subject!

Math

Share

THE orthogonal projection of a geometric figure on a line or plane corresponds to the set of points formed on the line, or plane, from the orthogonal (perpendicular) projection of each point of the figure on the line or plane.

You can think of orthogonal projection as the shadows of objects projected onto the ground during the midday sun, when the sun's rays are perpendicular to the ground.

Want to learn more? Check out a list of exercises on orthogonal projections, with all issues resolved.

Index

Exercises on orthogonal projections
Resolution of question 1
Resolution of question 2
Resolution of question 3
Resolution of question 4

Exercises on orthogonal projections

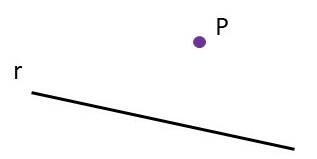
Question 1. Draw the orthogonal projection of point P on the line r in the figure below:

Question 2. Draw the segment's orthogonal projection $\dpi{100} \small \mathrm{\overline{AB}}$ on the line r of the figure below:

Question 3. Draw the orthogonal projection of the curve on the line r in the figure below: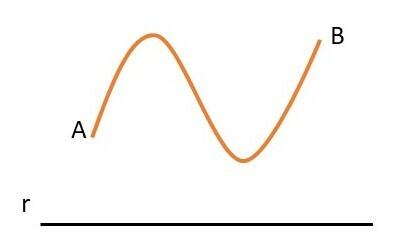

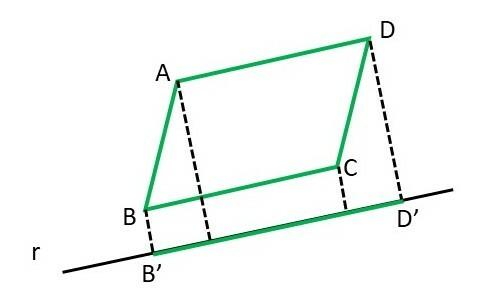
instagram story viewer

Question 4. Draw the orthogonal projection of the ABCD parallelogram on the line r in the figure below:

Resolution of question 1

Check out some free courses

Free Online Inclusive Education Course
Free Online Toy Library and Learning Course
Free Online Math Games Course in Early Childhood Education
Free Online Pedagogical Cultural Workshops Course

The orthogonal projection of point P on line r is a point P’, which corresponds to the end of the line segment with origin at P and which is perpendicular to line r.

Resolution of question 2

The orthogonal projection of the segment $\dpi{100} \small \mathrm{\overline{AB}}$ on the line r is a point A’ (which is equal to B’). This is because the thread $\dpi{100} \small \mathrm{\overline{AB}}$ is perpendicular to the line r.