Do you know how to calculate the area in the figure above? Probably when you learned how to calculate areas of geometric figures, you probably didn't learn any formula for calculating the area of a little house! But we can adapt this figure to make it more common and easier to work with. This little house was formed by pieces of tangram, an ancient Chinese puzzle. If we rearrange the tangram pieces, we can form more than 1000 figures, but without a doubt, the simplest format to calculate the area is the following image:
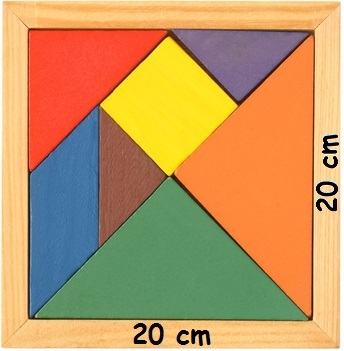
This square corresponds to the previous figure, the area of both are equal
In the image above there is a square formed with exactly the same pieces that made up the little house. Therefore, the area of the two figures will be the same. We will then calculate the area of the figures, using the last drawing. To calculate the area of a square, we must do:
Area = side x side
Area = 20 cm x 20 cm
Area = 400 cm²
So the area of the little house, as well as the area of any other figure formed by this tangram, will always be 400 cm². All figures that can be formed through the tangram can be called equidecomposable figures, as they are apparently distinct shapes, but which have the same area. Using this idea, we can calculate various geometric shapes, for example:

Do you know a way to calculate the area of this “L”-shaped concave polygon
All polygons, whether concave or convex, are equidecomposable figures. In the figure above, we have a concave polygon whose shape resembles an “L”. To calculate the area of this figure, we can decompose it into two known shapes, a square and a rectangle. In the figure, we highlight the square with blue color and the rectangle with orange color, so let's calculate its area:
Total area = rectangle area + square area
Total area = (base x height) + (side x side)
Total area = (4 cm x 12 cm) + (5 cm x 5 cm)
Total area = (48 cm²) + (25 cm²)
Total area = 73 cm²
Therefore, the area of the “L”-shaped polygon is 73 cm². Based on this principle of the areas of the equidecomposable figures, through decomposition, we can calculate the area of polygons without having to memorize formulas and more formulas. In the images below, let's see alternatives for calculating some areas:
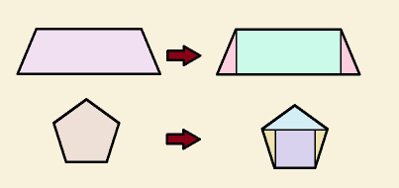
All polygons can be decomposed into equidecomposable figures
To obtain the area of the trapezoid, just decompose it into a rectangle and two triangles so that we can calculate the area of each of these shapes. The pentagon was decomposed into three triangles and a square, but it could have been decomposed into three triangles, for example, or any other shape that made it easier to calculate.
By Amanda Gonçalves
Graduated in Mathematics
Source: Brazil School - https://brasilescola.uol.com.br/matematica/Area-figuras-equidecomponiveis.htm
