The theorem proposed by Thales of Miletus takes into account that parallel lines cut by transversal lines give rise to proportional segments.
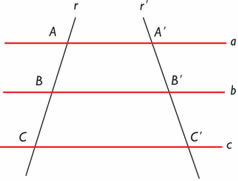
In the diagram, lines a, b and c are parallel and lines r and r’ are transverse. According to the Theorem, we have the following situations:
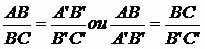
The situation involves knowledge of ratio and proportion, segment AB is proportional to segment BC; the segment A’B’ is proportional to the segment B’C’, as described in the 1st situation. Remember that this type of proportion is resolved through cross multiplication.
Example 1
In the following illustration, parallel lines r, s and t are intersected by transverse lines a and b, forming proportional segments. Apply Thales' Theorem and determine the value of the segment represented by x.

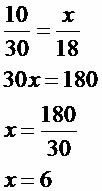
Example 2
Apply the property of Thales' Theorem and determine the value of the unknown x.
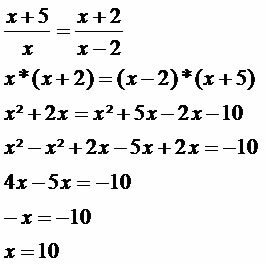
Thales' Theorem has several applications in the calculation of inaccessible distances. The approximate determination of distances between bodies in the solar system is made using proportionality.
by Mark Noah
Graduated in Mathematics
Brazil School Team
plane geometry - Math - Brazil School
Source: Brazil School - https://brasilescola.uol.com.br/matematica/proporcoes-aplicadas-no-teorema-tales.htm
