You compound interest are recurrent in Comercial relations, in long-term purchases in installments, in investments, in loans and even in the simple delay in paying bills. Interest can be an ally or a villain. It is important to master the factors that influence your calculation, which are principal, interest rate, time and amount.
When comparing compound interest with simple interest, we need to understand that the former is always calculated on the value of the previous year, the second is always calculated on top of the initial value. Compound interest will grow more over time compared to simple interest.
See too: Proportion - equality between two reasons
Compound interest formula
The calculation of compound interest is given by this formula:
M = C (1 + i)t |
Each of these letters is an important concept of the financial math:
Capital (C): is the first amount invested. We know as capital the initial value of the negotiation, that is, it is the reference value for calculating interest over time.
Interest (J): is the compensation value for income. When a financial institution makes a loan, it is abdicating itself from having this money in a certain period, however, when it receives it, its value will be corrected by what we call interest, and it is based on this that the company sees compensation for the loan. In an investment, this is the value of earned income.
Interest rate (i): and the percentage charged on top of the capital at every moment. This rate can be per day (a.d.), per month (a.m.), per two months (a.b.) or per year (a.a.). The interest rate is a percentage usually represented as a percentage, however, to calculate the compound interest, it is important to always write it in the decimal form.
Time (t): is the time the capital will be invested. It is important that the interest rate (i) and time (t) are always the same unit of measurement.
Amount (M): is the final transaction amount. The amount is calculated by adding principal plus interest — M = C + J.
How to calculate compound interest?
To know manipulate the formula it is fundamental to the study of compound interest. as there four variables (amount, capital, interest rate and time), the problems involving this theme can give the value of three of them and always ask for the calculation of the fourth variable, which can be any one of them. Hence the domain of equations it is critical to solving problems involving compound interest.
It is noteworthy that, to calculate the interest, it is necessary to know the capital and the amount, as the interest is given by the difference of the two, that is:
J = M - C |
Finding amount and interest
Example
A capital of R$1400 was applied to compound interest in an investment fund that yields 7% p.a. What interest will accrue after 24 months?
Resolution
Important data: C = 1400; i = 7% p.a.; t = 24 months.
Note that time and rate are in different units, but we know that 24 months equals 2 years, so t = 2 years, and that rate needs to be written in decimal form, i = 0.07.
M = C (1 + i) t
M = 1400 (1 + 0.07)²
M = 1400 (1.07)²
M = 1400. 1,1449
M = 1602.86.
To find the interest we have to:
J = M - C
1602,86 – 1400 = 202,86

finding the time
Example
How long does a capital of R$1500 applied to compound interest, at a rate of 10% p.a., take to generate an amount of R$1996.50?
Resolution
Since t is a power, we will find a exponential equation which can be solved by factoring or, in many cases, just by logarithm. As these are not always whole numbers, it is recommended for these problems to use a scientific calculator. In the case of entrance exams and competition exams, the value of the logarithm is given in the question.
Data:
C = 1500 M = 1996.50 i = 10% = 0.01

Finding the interest rate
Example
What is the interest rate applied per year for a capital of R$800 to generate interest of R$352 in two years?
Resolution
Data: C = 800; t = 2 years; J = 352.
To find the rate, we first need to find the amount.
M = C + J
800 + 352 = 1152
Now we have to:
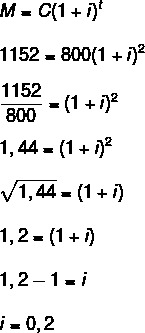
As a percentage, we can also say that i = 20%
Read too: Inversely proportional quantities - relationship such as speed and time
Difference between simple interest and compound interest
Simple interest uses a different formula from the one shown for compound interest:
J = C. i. t |
The difference between the behavior of simple interest and that of compound interest, in the short term, is quite subtle, but, over time, compound interest is much more advantageous.
turns out that O juros ssimple and always calculated on the initial value of the transaction. For example, if you apply $500 at 10% simple interest per month, that means that every month that capital will yield 10% of $500, that is, $50, no matter how long it stays there. Simple interest is common for overdue bills, such as water and energy. Each day of delay, the sum is given with a fixed amount calculated on top of the account.
already the juroscompound, thinking of the same amount and the same rate, in the first month, your income is calculated on top of the previous value. For example, in the first month, the 10% will be calculated on top of $500, generating $50 interest and an amount of $550. Next month, the 10% will be calculated on top of the current value of the amount, that is, 10% of R$550, generating an interest of R$55, and so on. Thus, for investments, compound interest is more advantageous. It is quite common exactly in this investment segment, such as savings.
See the comparative table of the same value yielding 10% a.m for one year to simple interest and compound interest.
Month |
simple interest |
compound interest |
0 |
BRL 1000 |
BRL 1000 |
1 |
BRL 1100 |
BRL 1100 |
2 |
BRL 1200 |
BRL 1210 |
3 |
BRL 1300 |
BRL 1331 |
4 |
BRL 1400 |
BRL 1464.10 |
5 |
BRL 1500 |
BRL 1610.51 |
6 |
BRL 1600 |
R$ 1771.56 |
7 |
BRL 1700 |
BRL 1948.72 |
8 |
BRL 1800 |
R$ 2143.59 |
9 |
BRL 1900 |
BRL 2357.95 |
10 |
BRL 2000 |
BRL 2593.74 |
11 |
R$ 2100 |
BRL 2853.12 |
12 |
R$ 2200 |
BRL 3138.43 |
solved exercises
Question 1 - How much will I be able to invest if I invest a capital of R$2000 at compound interest, of 3% p.a., during a period of 48 months?
Resolution
Data: C = 2000.00
i = 3% p.a.
t = 48 months = 4 years (note that the rate is in years)

Question 2 - To invest R$25,000, Maria quoted two options:
5% p.m. at simple interest
4% p.m. at compound interest
How long after is the second option more advantageous?
Resolution
To carry out the comparison, the table for calculating the interest of the first and second option follows:
Month |
1st option |
2nd option |
0 |
BRL 25,000 |
BRL 25,000 |
1 |
BRL 26,250 |
BRL 26,000 |
2 |
BRL 27,500 |
BRL 27,040 |
3 |
BRL 28,750 |
BRL 28,121.60 |
4 |
BRL 30,000 |
BRL 29,246.46 |
5 |
BRL 31,250 |
BRL 30,416.32 |
6 |
BRL 32,500 |
BRL 31,632.98 |
7 |
BRL 33,750 |
BRL 32,898.29 |
8 |
BRL 35,000 |
BRL 34,214.23 |
9 |
BRL 36,250 |
BRL 35,582.80 |
10 |
BRL 37,500 |
BRL 37,006.11 |
11 |
BRL 38,750 |
BRL 38,486.35 |
12 |
BRL 40,000 |
BRL 40,025.81 |
When comparing the two options, the second is perceived as more advantageous for investments over 11 months.
By Raul Rodrigues de Oliveira
Maths teacher
Source: Brazil School - https://brasilescola.uol.com.br/matematica/juros-compostos.htm
