O determinant of a headquarters has several applications currently. We use the determinant to check if three points are aligned in the Cartesian plane, to calculate areas of triangles, for solving linear systems, among other applications in math. The study of determinants not limited to math, there are some applications in physics, such as the study of electric fields.
We calculate determinants of square matrices only., that is, matrices in which the number of columns and the number of rows are equal. To calculate the determinant of a matrix, we need to analyze its order, that is, if it is 1x1, 2x2, 3x3 and so on, the higher your order, the harder it will be to find the determinant. However, there are important methods of performing the exercise, such as Sarrus' rule, used to calculate determinants of 3x3 matrices.
Read too: Process for solving an m x n linear system
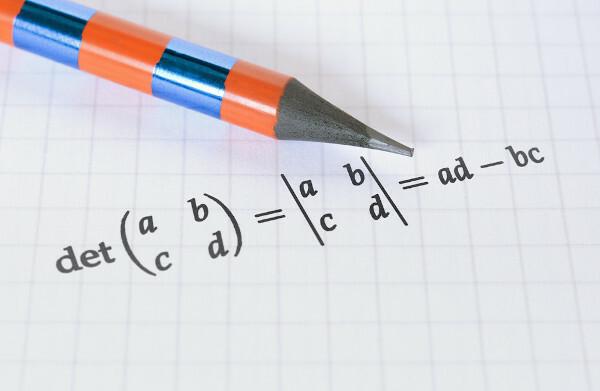
Matrix determinant of order 1
An array is known as order 1 when it has exactly
a row and a column. When this occurs, the matrix has a single element, the a11. In this case, the matrix determinant coincides with its only term.A = (a11)
det(A) = | The11 | = the11
Example:
A = [2]
det(A) = |2| = 2
In order to calculate determinants of matrices of order 1, it is only necessary to know their single element.
Do not stop now... There's more after the advertising ;)
Determinants of order 2 matrices
The 2x2 square matrix, also known as the order 2 matrix, has four elements, in this case, to calculate the determinant, it is necessary to know what the main diagonal and the secondary diagonal.
To calculate the determinant of an order 2 matrix, we calculate thedifference enter the product of the terms of main diagonal and the terms of secondary diagonal. Using the algebraic example we built, det (A) will be:

Example:

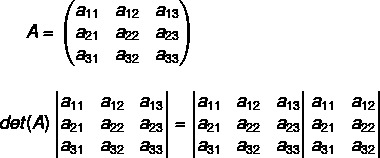
Matrix determinant of order 3
The order three matrix is more laborious to obtain the determinant than the previous ones, in fact, the higher the order of a matrix, the more difficult this work will be. In it is necessary use what we know as Sarrus' rule.
Sarrus' Rule
Sarrus' rule is a method for calculating determinants of matrices of order 3. It is necessary to follow a few steps, being the first duplicate the first two columns at the end of the matrix, as shown in the following example.
Let's go now multiply the terms of each of the three diagonals that are in the same direction as the main diagonal.

We will carry out a similar process with the secondary diagonal and the other two diagonals that are in the same direction as it.

note that the terms of the secondary diagonal are always accompanied by the minus sign., that is, we will always change the sign of the result of multiplying the secondary diagonal terms.
Example:

See too: Binet's Theorem - practical process for matrix multiplication
Determinant properties
1st property
If one of the lines of the matrix is equal to 0, then its determinant will be equal to 0.
Example:

2nd property
Let A and B be two matrices, det (A·B) = det (A) · det (B).
Example:
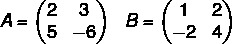
Calculating the separate determinants, we have to:
det (A) = 2 · (-6) – 5 · 3
det (A) = -12 – 15 = -27
det (B) = 4 · 1 – 2 · (-2)
det (B) = 4 + 4 = +8
So det (A) · det (B) = -27 · 8 = -216
Now let's calculate det (A·B)

3rd property
Let A be a matrix and A’ a new matrix constructed by swapping the rows of matrix A, then det (A’) = -det (A), or that is, when reversing the position of the lines of a matrix, its determinant will have the same value, but with a sign exchanged.
Example:

4th property
equal lines or proportional make the matrix determinant equal to 0.
Example:
Note that in matrix A, the terms in row two are twice the terms in row one.

Also access:Application of matrices in entrance exams
solved exercises
Question 1 - (Vunesp) Considering matrices A and B, determine the value of det (A·B):

to 1
b) 6
c) 10
d) 12
e) 14
Resolution
Alternative E
We know that det (A·B) = det (A) · det (B):
det (A) = 1· 4 – 2 · 3 = 4 – 6 = -2
det (B) = -1 · 1 – 3 · 2 = -1 – 6 = -7
So we have to:
det (A·B) = det (A) · det (B)
det (A·B) = -2 (-7) = 14
Question 2 - Given matrix A, what must be the value of x for det(A) to be equal to 0?
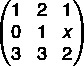
a) 1/2
b) 1/3
c) 1/9
d) 3
e) 9
Resolution
Alternative B
Calculating the determinant of A, we have to:
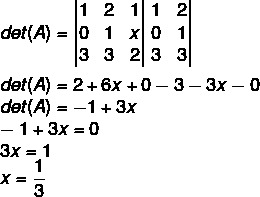
By Raul Rodrigues de Oliveira
Maths teacher
Would you like to reference this text in a school or academic work? Look:
OLIVEIRA, Raul Rodrigues de. "Determinants"; Brazil School. Available in: https://brasilescola.uol.com.br/matematica/determinantes-1.htm. Accessed on June 29, 2021.
Matrix, Type of matrices, Order of matrices, Row matrix, column matrix, Null matrix, Matrix square, Diagonal matrix, Identity matrix, Opposite matrix, Matrix, equal matrix, Equality of matrices.