For the calculation of determinants of square matrices of order less than or equal to 3 (n≤3), we have some practical rules to perform these calculations. However, when the order is greater than 3 (n>3), many of these rules are not applicable.
So we will see Laplace's theorem, which, using the concept of the cofactor, leads the calculation of determinants to rules that apply to any square matrices.
Laplace's theorem consists of choosing one of the rows (row or column) of the matrix and adding the products of the elements of that row by their respective cofactors.
Algebraic illustration:

Let's look at an example:
Calculate the determinant of matrix C using Laplace's theorem:
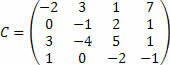
According to Laplace's theorem, we must choose a row (row or column) to calculate the determinant. Let's use the first column:

We need to find the cofactor values:
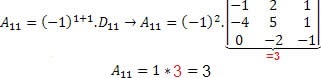


Thus, by Laplace's theorem, the determinant of matrix C is given by the following expression:
Do not stop now... There's more after the advertising ;)

Note that it was not necessary to calculate the cofactor of the matrix element which was equal to zero, after all, when we multiply the cofactor, the result would be zero anyway. Therefore, when we come across matrices that have many zeros in one of their rows, the use of Laplace's theorem becomes interesting, as it will not be necessary to calculate several cofactors.
Let's look at an example of this fact:
Calculate the determinant of matrix B using Laplace's theorem:

Note that the second column is the row that has the largest amount of zeros, so we will use this row to calculate the matrix determinant through Laplace's theorem.

Therefore, to determine the determinant of matrix B, just find the cofactor A22.
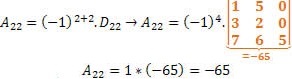
Therefore, we can complete the calculations of the determinant:
det B = (- 1). (- 65) = 65
By Gabriel Alessandro de Oliveira
Graduated in Mathematics
Brazil School Team
Would you like to reference this text in a school or academic work? Look:
OLIVEIRA, Gabriel Alessandro de. "Laplace's Theorem"; Brazil School. Available in: https://brasilescola.uol.com.br/matematica/teorema-laplace.htm. Accessed on June 29, 2021.