We know how polynomial an expression that indicates the algebraic sum of monomials that are not similar, that is, polynomial is one algebraic expression between monomials. Monomium is an algebraic term that has a coefficient and a literal part.
When there are similar terms between the polynomials, it is possible to perform the reduction of its terms in addition and/or subtraction of two polynomials. It is also possible to multiply two polynomials through the distributive property. The division is performed using the keys method.
Read too: Polynomial Equation - Equation characterized by having a polynomial equal to 0
What are monomials?
To understand what a polynomial is, it is important to first understand the meaning of a monomial. An algebraic expression is known as a monomium when it has numbers and letters and their exponents separated only by multiplication. The number is known as the coefficient, and the letters and their exponents are known as the literal part.
Examples:
2x² → 2 is the coefficient; x² is the literal part.
√5ax → √5 is the coefficient; ax is the literal part.
b³yz² → 1 is the coefficient; b³yz² is the literal part.
What is a polynomial?
A polynomial is nothing but the algebraic sum of monomials, that is, they are more monomials separated by addition or subtraction from each other.
Examples:
ax² + by + 3
5c³d – 4ab + 3c²
-2ab + b – 3xa
Generally speaking, a polynomial can have several terms, it is represented algebraically by:
Thenoxno + the(n-1) x(n-1) + … + the2x² + a1x + a
See too: What are the classes of polynomials?
degree of a polynomial
To find the degree of the polynomial, let's separate it into two cases, when it has a single variable and when it has more variables. The degree of the polynomial is given by the degree of the greatest of its monomials in both cases.
It is quite common to work with a polynomial that has only one variable. When that happens, O greater monomium degree which indicates the degree of the polynomial is equal to the largest exponent of the variable:
Examples:
Single Variable Polynomials
a) 2x² – 3x³ + 5x – 4 → note that the variable is x, and the largest exponent it has is 3, so this is a degree 3 polynomial.
b) 2y5 + 4y² – 2y + 8 → the variable is y, and the largest exponent is 5, so this is a polynomial of degree 5.
When the polynomial has more than one variable in a monomial, to find the degree of this term, it is necessary add-if the degree the exponents of each of the variables. Thus, the degree of the polynomial, in this case, is still equal to the degree of the largest monomial, but it is necessary to take care to add the exponents of the variables of each monomial.
Examples:
a) 2xy + 4x²y³ – 5y4
Analyzing the literal part of each term, we have to:
xy → grade 2 (1 + 1)
x²y³ → degree 5 (2 + 3)
y³ → grade 3
Note that the largest term has degree 5, so this is a degree 5 polynomial.
b) 8a²b - ab + 2a²b²
Analyzing the literal part of each monomium:
a²b → grade 3 (2 + 1)
ab² → degree 2 (1 + 1)
a²b² → grade 4 (2 + 2)
Thus, the polynomial has degree 4.
Adding Polynomials
To the addition between two polynomials, let's carry out the reduction of similar monomials. Two monomials are similar if they have equal literal parts. When this happens, it is possible to simplify the polynomial.
Example:
Let P(x) = 2x² + 4x + 3 and Q(x) = 4x² – 2x + 4. Find the value of P(x) + Q(x).
2x² + 4x + 3 + 4x² - 2x + 4
Finding similar terms (which have the same literal parts):
2x² + 4x + 3 + 4x² – 2x + 4
Now let's add the similar monomials:
(2+4)x² + (4-2)x + 3 + 4
6x² + 2x +7
Polynomial Subtraction
Subtraction is not much different from addition. The important detail is that first we need to write the opposite polynomial before we carry out the simplification of similar terms.
Example:
Data: P(x) = 2x² + 4x + 3 and Q(x) = 4x² - 2x + 4. Calculate P(x) – Q(x).
The polynomial -Q(x) is the opposite of Q(x), to find the opposite of Q(x), just reverse the sign of each of its terms, so we have to:
-Q(x) = -4x² +2x – 4
Then we will calculate:
P(x) + (-Q(x))
2x² + 4x + 3 - 4x² + 2x - 4
Simplifying similar terms, we have:
(2 - 4)x² + (4 + 2)x + (3 - 4)
-2x² + 6x + (-1)
-2x² + 6x – 1
Polynomial Multiplication
To perform the multiplication of two polynomials, we use the known distributive property between the two polynomials, operating the multiplication of the monomials of the first polynomial by those of the second.
Example:
Let P(x) = 2a² + b and Q(x) = a³ + 3ab + 4b². Calculate P(x) · Q(x).
P(x) · Q(x)
(2a² + b) (a³ + 3ab + 4b²)
Applying the distributive property, we will have:
2a² · a³ + 2a² · 3ab + 2a² · 4b² + b · a³ + b · 3ab + b · 4b²
2nd5 + 6a³b + 8a²b² + a³b + 3ab² +4b³
Now, if they exist, we can simplify similar terms:
2nd5 + 6a³b + 8a²b² + ab + 3ab² + 4b³
Note that the only similar monomials are highlighted in orange, simplifying between them, we will have the following polynomial as an answer:
2nd5 + (6+1)ab + 8a²b² + 3ab² + 4b³
2nd5 + 7a³b + 8a²b² + 3ab² + 4b³
Also access: How to do algebraic fraction multiplication?
polynomial division
perform the division of polynomials can be quite laborious, we use what is called keys method, but there are several methods for this. The division of two polynomials it is only possible if the degree of the divisor is smaller. By dividing the polynomial P(x) by the polynomial D(x), we are looking for a polynomial Q(x), such that:
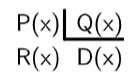
Thus, by the division algorithm, we have: P(x) = D(x) · Q(x) + R(x).
P(x) → dividend
D(x) → divider
Q(x) → quotient
R(x) → remainder
When operating the division, the polynomial P(x) is divisible by the polynomial D(x) if the remainder is zero.
Example:
Let's operate by dividing the polynomial P(x) = 15x² +11x + 2 by the polynomial D(x) = 3x + 1.
We want to share:
(15x² + 11x + 2): (3x + 1)
1st step: we split the first monomium of the dividend with the first of the divisor:
15x²: 3x = 5x

2nd step: we multiply 5x · (3x+1) = 15x² + 5x, and subtract the result of P(x). To perform the subtraction, it is necessary to invert the signs of the multiplication result, finding the polynomial:
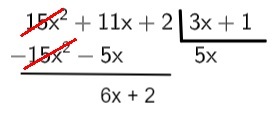
3rd step: we perform the division of the first term of the subtraction result by the first term of the divisor:
6x: 3x = 2
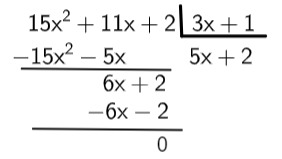
4th step: so we have (15x² + 11x + 2): (3x + 1) = 5x + 2.
Therefore, we have to:
Q(x) = 5x + 2
R(x) = 0
Read too: Briot-Ruffini's practical device – division of polynomials
solved exercises
Question 1 - What should the value of m be so that the polynomial P(x) = (m² – 9)x³ + (m + 3)x² + 5x + m has degree 2?
A) 3
B) -3
C) ±3
D) 9
E) -9
Resolution
Alternative A
For P(x) to have degree 2, the coefficient of x³ must be equal to zero, and the coefficient of x² must be different from zero.
So we will do:
m² - 9 = 0
m² = 9
m = ± 9
m = ±3
On the other hand, we have that m + 3 ≠ 0.
So, m ≠ -3.
Thus, we have as a solution of the first equation that m = 3 or m= -3, however, for the second, we have m ≠ -3, so the only solution that makes P(x) have degree 2 is: m = 3.
Question 2 - (IFMA 2017) The perimeter of the figure can be written by the polynomial:

A) 8x + 5
B) 8x + 3
C) 12 + 5
D) 12x + 10
E) 12x + 8
Resolution
Alternative D
From the image, when we analyze the given length and width, we know that the perimeter is the sum of all sides. Since the length and height are the same, we just multiply the sum of the given polynomials by 2.
2 · (2x + 1 + 4x + 4) = 2 · (6x + 5) = 12x + 10
By Raul Rodrigues de Oliveira
Maths teacher

