O Thesimple arrangement is a type of grouping studied in combinatorial analysis. We know how to arrange all groupings formed with no elements taken from k in k, knowing that the value of no > k.
To differentiate the arrangement from the other groupings (the combination and the permutation), it is important to understand that, in the combination, the order of the elements in the set is not important and that, in the arrangement, it is. Furthermore, in the permutation, all the elements of the set are involved, since in the arrangement, we chose part of the set, in this case, expressed by k elements of the set.
To calculate any of these groups and, in particular, the arrangement, it is necessary to use specific formulas for each one of them. There are several arrangement applications, one of which is in the elaboration of bank passwords. Ever wonder how many passwords it is possible to create with certain numbers and letters? It is through arrangement that we are able to answer this question.
Read too: What is the fundamental principle of counting?

What is the formula for the simple arrangement?
There are arrangement problems where it is not necessary to use the formula, because they are simple problems. For example, given the set {a, b, c}, how many different ways can we choose 2 elements of this set so that order is important?
To solve this problem, just rewritemos the possible groupings. This is an arrangement because we are taking sequences of 2 elements from a set that has 3 elements. Possible arrangements are:
A{(a, b); (b, a); (a, c); (c, a); (a, d); (gives); (b, c); (c, b); (b, d); (d, b); (CD); (d, c)}
In this case we can say that there are 12 possible arrangements, with 3 elements taken from 2 in 2. Often the interest is in the number of possible arrangements and not on the list, as we did earlier.
To solve arrangement problems, that is, find how many arrangements there are of no elements taken from k in k, we use the following formula:

How to calculate the simple arrangement?
To count the number of arrangements in a given situation, just identify how many elements have on the whole and how many elements will be chosen of this set, that is, what is the value of no and what is the value of k in this situation, later, just replace the values found in the formula and calculate the factorials.
Do not stop now... There's more after the advertising ;)
Example 1:
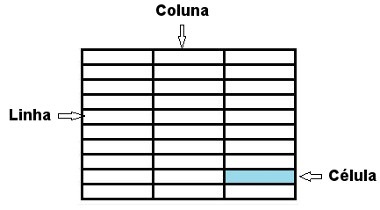
How many arrangements are there of 9 elements taken from 3 to 3?
no = 9 and k = 3
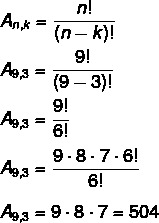
Example 2:
The passwords for a given bank consist of four digits, and the numbers used could not appear twice in the same password. So, what is the number of possible passwords for this system?
We're dealing with an array problem because, in a password, order is important, and there are 10 digit choices (all numbers 0 through 9), from which we'll choose 4.
no = 10
k = 4
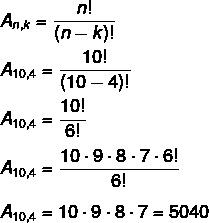
Read too: Additive counting principle — union of one or more sets
Simple arrangement and simple combination
for those who are studying combinatorial analysis, one of the most important points is the differentiation between problems that can be solved with simple arrangement and problems that can be solved with simple combination. Although they are close concepts and used to calculate the total number of possible groupings in a part of the elements of the set, to differentiate problems involving them, just analyze whether, in the proposed problem, the order is important or not.
When order is important, the problem is resolved through an arrangement. Arrangement (A, B) is a different grouping from (B, A). Thus, problems involving queues, podiums, passwords or any other situation in which, when moving the order of the elements, different groupings are formed, they are solved using the formula of arrangement.
When order is not important, the problem is solved through a combination. The combination {A, B} is the same grouping as {B, A}, ie the order of the elements is irrelevant. Problems involving drawing, samples of a set, among others, in which the order is not relevant, are solved using the combination formula. To learn more about this other form of grouping, read: simple combination.
solved exercises
Question 1 - Chess emerged in the sixth century, in India, reaching other countries, such as China and Persia, and becoming one of the games of most popular board of today, being practiced by millions of people and existing tournaments and competitions international. The game is played on a square board and divided into 64 squares, alternately white and black. On one side are the 16 white pieces, and on the other, the same number of black pieces. Each player is entitled to one move at a time. The objective of the game is to checkmate the opponent. In an international competition, the top 15 chess players are equally capable of reaching the final and being the winner. Knowing that, in how many different ways can the podium in this competition happen?
A) 32,760
B) 455
C) 3510
D) 2730
E) 210
Resolution
Alternative D
We have to no = 15 and k = 3.
Question 2 - (Enem) Twelve teams signed up for an amateur soccer tournament. The opening game of the tournament was chosen as follows: first, 4 teams were drawn to make up Group A. Then, among the teams in Group A, 2 teams were drawn to play the opening game of the tournament, the first of which would play in their own field, and the second would be the visiting team. The total number of possible choices for Group A and the total number of choices for the teams in the opening game can be calculated using:
A) a combination and an arrangement, respectively.
B) an arrangement and a combination, respectively.
C) an arrangement and a permutation, respectively.
D) two combinations.
E) two arrangements.
Resolution
Alternative A. To know what kind of grouping the problem is referring to, it is enough to analyze whether the order is important or not.
In the first grouping, 4 teams will be drawn among the 12. Note that, in this draw, the order does not matter. Regardless of the order, the 4 drawn teams will make up Group A, so the first grouping is a combination.
In the second choice, of the 4 teams, 2 will be drawn, but the first will play at home, so, in this case, the order generates different results, thus, it is an arrangement.
By Raul Rodrigues Oliveira
Maths teacher