Linear systems are formed by a set of linear equations of m unknowns. All systems have a matrix representation, that is, they constitute matrices involving the numerical coefficients and the literal part. Note the matrix representation of the following system:  .
.
Incomplete matrix (numerical coefficients)
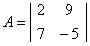
full matrix

Matrix representation

The relationship between a linear system and a matrix consists of solving systems using the Cramer method.
Let's apply Cramer's rule in solving the following system: 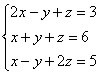 .
.
We apply Cramer's rule using the incomplete matrix of the linear system. In this rule we use Sarrus to calculate the determinant of the established matrices. Note the determinant of the systems matrix:

Do not stop now... There's more after the advertising ;)
Sarrus' rule: sum of the products of the main diagonal subtracted from the sum of the products of the minor diagonal.
Replace the 1st column of the systems matrix with the column formed by the independent terms of the system.

Replace the 2nd column of the systems matrix with the column formed by the independent terms of the system.
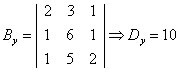
Replace the 3rd column of the systems matrix with the column formed by the independent terms of the system.

According to Cramer's rule, we have:

Therefore, the solution set of the system of equations is: x = 1, y = 2 and z = 3.
by Danielle de Miranda
Graduated in Mathematics
Brazil School Team
Matrix and Determinant - Math - Brazil School
Would you like to reference this text in a school or academic work? Look:
SILVA, Marcos Noé Pedro da. "Relationship between Matrix and Linear Systems"; Brazil School. Available in: https://brasilescola.uol.com.br/matematica/relacao-entre-matriz-sistemas-lineares.htm. Accessed on June 29, 2021.


