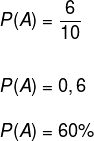THE probability is a branch of math who studies ways of how estimate the chance of a certain event happening. For example, imagine that we have an urn with 10 white balls and 20 red balls. Certainly the chance of getting a red ball is much higher, however that doesn't mean that we're going to get a red ball on the first try, as there are also white balls. The study of probability allows you to measure the chance of getting red balls or white balls by associating this chance with a real number.
Read too: Likelihood of a complementary event
Probability Basics
random experiment
Random experiments are those that, when repeated several times and keeping the processes running, result in unlikely results. For example, when we flip a coin ten times in a row, the results are unlikely, as with each flip, either a heads or tails may appear.
Sample space
Let's call the sample space the set of all possible results of a given phenomenon or from random experiment.
Examples
a) When flipping a coin, the possible results are heads or tails, so the sample space is:
AND1 = {heads, tails}
B)When rolling an honest die, the possible results are the six sides of the dice, so:
AND2 = {1, 2, 3, 4, 5, 6}
c) A coin is flipped twice, so the sample space is determined by the pairs ordered in which the first element represents the result of the first throw and the second represents the result of the second throw, thus:
E = {(c, c), (c, k), (k, k), (k, c)}
c → Crown
k → Dude
Event
An event is every subset of a sample space.
Examples
Consider the sample space of a die roll, so E = {1,2,3,4,5,6}. The following cases are examples of events:
a) Event in which faces are greater than 3. We will denote such an event by A, hence:
A = {4, 5, 6}
Generally speaking, we can write such an event using set notation:
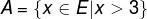
Note that every element of A is an element of the set E, so A is a subset of E.
b) Event in which the faces are odd numbers. In this case, we will denote such an event by B, like this:
B = {1, 3, 5}

Equiprobable spaces
Consider a sample space E and also a random experiment from that space. Let's say E is a equiprobable sample space if all the events in the experiment have the same probability of happening.
Examples
Imagine an urn with just two balls, one white and one black. The chance of taking a cue ball is the same as taking a black ball, so the sample space is equiprobable.
Another example is the birth of a baby. The chance of being a boy is the same as the chance of being a girl, so this event has an equiprobable sampling space.
See too: Probability: Basic Definitions
Probability formula and calculation
The probability of a given event A, represented by P(A), is the division between the number of favorable cases and the number of possible cases. We can represent, then, the chance of event A to occur by:
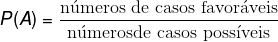
Example
Let's determine the probability that we get a cue ball in an urn with 10 white balls and 20 red balls.
For this, we will initially determine the number of favorable cases and the number of possible cases.
Favorable cases → 10 (white balls)
Possible cases → 10 + 20 (white balls + red balls)
Note that favorable cases are the cases that interest us – in this case, the number of white balls – and possible cases represent the total number of elements in the sample space. Let's call the event in question A, like this:

The chance of getting a cue ball is therefore 33.33%.

Exercises
question 1 – (UFPE) A letter is chosen at random among those that make up the word PERNAMBUCO. How likely is it to be a consonant?
Solution
Note that the total number of letters in the word PERNAMBUCO is equal to 10. The favorable case in this problem is the number of consonants, which are 6. Therefore, the probability of choosing a consonant is: