The inverse of a number is the exchange of the numerator for the denominator and vice versa, as long as that fraction or number is different from zero. In a complex number it happens the same way: a complex number to have its inverse must be non-null, for example:
Given any non-zero complex number z = a + bi, its inverse will be represented by z–1.
See the calculation of the inverse of the complex number z = 1 – 4i. 
Therefore, the inverse of the complex number z = 1 – 4i will be: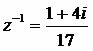
We conclude that the inverse of a non-zero complex number will have the following generality: z = a + bi 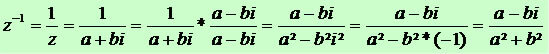
When we multiply a complex number by its inverse the result will always be equal to 1, z * z–1 = 1. Note the multiplication of the complex z = 1 – 4i by its inverse: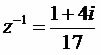
Multiplication of complex numbers occurs as follows:
(a+bi)*(c +di) = ac + adi + bci + bdi² = ac + (ad + bc) i + bd(–1) = ac + (ad + bc) i – bd = (ac – bd) + (ad + bc) i 
Do not stop now... There's more after the advertising ;)
by Mark Noah
Graduated in Mathematics
Brazil School Team
Complex numbers - Math - Brazil School
Would you like to reference this text in a school or academic work? Look:
SILVA, Marcos Noé Pedro da. "Inverse of a complex number"; Brazil School. Available in: https://brasilescola.uol.com.br/matematica/inverso-um-numero-complexo-1.htm. Accessed on June 29, 2021.


