Thales' Theorem is a principle of geometry that states that there are proportional segments present in a bundle of parallel lines when cut by transverse lines.
This theorem was created by Thales of Miletus, an important Greek mathematician, philosopher and astronomer who observing the shadows of a pyramid, found proportionality between the measure of these shadows and the height of the pyramid.
Step by step for interpreting Thales' Theorem
In order for you to better understand the concept of Thales' Theorem, you need to consider the following information:
- One beam of parallel lines there are 3 or more lines arranged in parallel, as in the example below;

- One cross straight is the line that cuts parallel lines, like the t line in the image below;

- One straight segment is the part of a line determined by two points. The segments on the line r in the image below are: AB, CD and the larger segment AD;

- THE reason designates the comparison between two quantities. Pay attention to the example:
If in a mathematical problem you have the magnitudes 60 and 20, what is the ratio between them? To find out, apply:
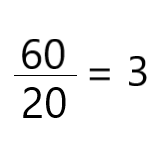
The ratio between the magnitudes 60 and 20 is 3.
Heads up: within the reason there is a quantity that will be antecedent (numerator) and another consequential (denominator). To find out the position of each one, always pay attention to the statement of the question or the information provided.
- Proportion is when two ratios are the same;
All this step-by-step information above is important for you to understand and analyze a Thales' Theorem. In the example below, understand how the concept of proportion of lines works.
Thales Theorem Example
In the image below, we can evaluate a Thales' Theorem. See that it contains a bundle of 3 lines (The,B and ç), 2 transversal lines (r and r'), and some straight segments, such as AB or A'C'.

What makes it a Thales' Theorem is that the straight lines present in the image are proportional. To find this out, we have to see if the present reasons are proportional. In the image above, for example, we can see that:
{A\B = A’\B'} and {B\C = B’\C’}
It reads:
- The line segment A\B is proportional to the line segment A’\B’, since their ratios are equal.
- The line segment B\C is proportional to the line segment B’\C’, since their ratios are also equal.
These are not the only proportional segments within the theorem. You can also find the following reason:
{A\C = A’\C’}
In this case, it reads:
- Line segment A\C is proportional to line segment A'\B', since their ratios are equal.
Example of Thales' Theorem in triangles
The Tales Theorem can also be applied to situations with triangles. In the image below, for example, it can be concluded that:
- Line segments DE and BC are proportional.
- Therefore, we can the triangles ABC and ADE are also proportional.

In this case, it is represented as follows:
Δ ABC ~ Δ AED
See also the meaning of:
- Parallel Lines;
- Bisector.