We know how progressions particular cases of number sequences. There are two cases of progressions:
arithmetic progression
geometric progression
To be a progression, we need to analyze the characteristics of the sequence for if there is what we call a reason. when the progression is arithmetic, the reason is nothing more than a constant that we add to a term to find its successor in the sequence; now, when working with a progression geometric, reason has a similar function, only in this case reason is the constant term by which we multiply a term in the sequence to find its successor.
Due to predictable behavior of a progression, there are specific formulas for finding any term in these sequences, and it is also possible to develop a formula for each of them (that is, one for the arithmetic progression and one for the geometric progression) in order to calculate the sum Fromno first terms of this progression.
Read too: Functions – what are they and what are they for?

number sequence
To understand what progressions are, we first need to understand what they are number sequences. As the name suggests, we know the number sequence a set of numbers that respect an order, being well defined or not. Unlike the sets numerics where order does not matter, in a numeric sequence, order is essential, for example:
The sequence (1, 2, 3, 4, 5) is different from (5, 4, 3, 2, 1), which is different from the sequence (1, 5, 4, 3, 2). Even if the elements are the same, as the order is different, so we have different sequences.
Examples:
We can write sequences whose formations are easy to see:
a) (0, 2, 4, 6, 8, 10, 12) → sequence of even numbers less than or equal to 12.
b) (17, 15, 13, 11, 9, 7, 5) → regressive sequence of odd numbers from 17 to 5.
c) (1, 1, 2, 3, 5, 8, 13 …) → known as Fibonacci sequence.
d) (1, -1, 2, -2, 3, -3, 4, -4 …) → although it is not possible to describe this sequence like the others, it is easy to predict what its next terms will be.
In other cases, the sequences can have total randomness in their values, in any case, to be a sequence, what matters is to have a set of ordered values.
to 1; 0,1; 0,02; 0,07; 0,0001; 7)
b) (2, 3, -3, 2, 6, 4, 8, -2 ...)
As much as it is not possible to predict who the next terms in the letter b are, we are still working with a sequel.
In general, strings are always represented in parentheses ( ), in the following way:
(The1, a2,The3, a4,The5, a6, a7, a8 …) → infinite sequence
(The1, a2,The3, a4,The5, a6, a7, a8 … ano) → finite sequence
In both, we have the following representation:
The1 → first term
The2 → second term
The3 → third term
.
.
.
Theno → nth term
Observation: It is of great importance that, when representing a sequence, the data is enclosed in parentheses. Sequence notation is often confused with set notation. A set is represented in braces, and in the set the order is not important, which makes all the difference in this case.
(1, 2, 3, 4, 5) → sequence
{1, 2, 3, 4, 5} → set
There are particular cases of sequence that are known as progressions.
See too: What is the fundamental principle of counting?
What are progressions?
A sequence is defined as a progression when it has a regularity from one term to another, known as reason. There are two cases of progression, arithmetic progression and geometric progression. To know how to differentiate each of them, we need to understand what the reason for a progression is and how that reason interacts with the terms of the sequence.
When, from one term to the other in the sequence, I have a constant sum, this sequence is defined as a progression, and in this case it is a arithmetic progression. This value that we are constantly adding up is known as the ratio. The other case, that is, when the sequence is a geometric progression, from one term to another there is a multiplication by a constant value. Analogously, this value is the ratio of the geometric progression.
Examples:
a) (1, 4, 7, 10, 13, 16 …) → notice that we are always adding 3 from one term to the other, so we have an arithmetic progression of ratio equal to 3.
b) (1, 10, 100, 1000, 10000 …) → in this case we are always multiplying by 10 from one term to the other, dealing with a geometric progression of ratio 10.
c) (0, 2, 8, 26 …) → in the latter case, there is only one sequence. To find the next term, we multiply the term by 3 and add 2. This case, even though there is a regularity to find the next terms, it is just a sequence, not an arithmetic or geometric progression.
arithmetic progression
When we work with number sequences, those sequences in which we can predict their next terms are quite recurrent. For this sequence to be classified as a arithmetic progression, there needs to be a reason a. From the first term, the next term is constructed by the sum of the previous term with the reason r.
Examples:
a) (4, 7, 10, 13, 16, 19, 22, 25...)
This is a sequence that can be classified as arithmetic progression, because the reason r = 3 and the first term is 4.
b) (7, 2, -3, -8, -13, -18, -23 …)
This sequence is an arithmetic progression with good reason. r = -5, and its first term is 7.
Terms of a PA
In many cases, our interest is to find a specific term in the progression, without having to write the entire sequence. Knowing the value of the first term and the ratio, it is possible to find the value of any term in an arithmetic progression. To find the terms of an arimetic progression, we use the formula:
Theno = the1+ (n - 1)r
Example:
Find the 25th term of a P.A whose ratio is 3 and first term is 12.
Data r = 3, the1 = 12. We want to find the 25th term, that is, n = 25.
Theno = the1+ (n - 1)r
The25 = 12 + (25 - 1) · 3
The25 = 12 + 24 · 3
The25 = 12 + 72
The25 = 84
General term of a P.A.
The general term formula is a way to simplify the formula of an AP term to find any progression term more quickly. Once the first term and the reason are known, it is enough to substitute in the formula a term of a P.A., in order to find the general term of the arithmetic progression, which depends only on the value of no.
Example:
Find the general term of a P.A. that has r = 3 and the1 = 2.
Theno = 2 + (n -1) r
Theno = 2 + (n -1) 3
Theno = 2 + 3n – 3
Theno = 2n - 1
This is the general term of a P.A., which serves to find any term in this progression.
Sum of terms of a PA
THE sum of terms of a PA it would be quite laborious if it were necessary to find each of its terms and add them up. There is a formula for calculating the sum of all no first terms of an arithmetic progression:

Example:
Find the sum of all odd numbers from 1 to 100.
We know that odd numbers are an arithmetic progression of ratio 2: (1, 3, 5, 7…99). In this progression there are 50 terms, since, from 1 to 100, half of the numbers are even and the other half is odd.
Therefore, we have to:
n = 50
The1 = 1
Theno = 99

Also access: 1st degree function - practical use of arithmetic progression
Geometric progression
A string can also be classified as progression geometric (PG). For a sequence to be a geometric progression, it needs to have a reason, but in this case, to find the next term from the first term, we perform the multiplication of ratio by previous term.
Examples:
a) (3, 6, 12, 24, 48 …) → Geometric progression of ratio 2, and its first term is 3.
b) (20, 200, 2000, 20 000 …) → Geometric progression of ratio 10, and its first term is 20.
Term of a PG
In a geometric progression, we represent the reason for the letter what. The term of a geometric progression can be found by the formula:
Theno = the1 · whatn - 1
Example:
Find the 10th term of a PG, knowing that what = 2 and the1 = 5.
Theno = the1 · whatn - 1
The10 = 5 · 210 - 1
The10 = 5 · 29
The10 = 5 · 512
The10 = 2560
General term of a PG
When we know the first term and the reason, it is possible to generate the general term formula from a geometric progression that depends exclusively on the value of no. For this, we just need to replace the first term and the ratio, and we will find an equation that depends only on the value of no.
Using the previous example, where the ratio is 2 and the first term is 5, the general term for this GP is:
Theno = the1 · whatn - 1
Theno = 5 · 2n - 1
Sum of terms of a PG
Adding all the terms of a progression would be a lot of work. In many cases, writing the entire sequence to accomplish this sum is time-consuming. To facilitate this calculation, the geometric progression has a formula that serves to calculate the sum of no first elements of a finite PG:

Example:
Find the sum of the first 10 terms of the GP (1, 2, 4, 8, 16, 32 …).
Note that the ratio of this PG is equal to 2.
The1 = 1
what = 2
no = 10

Read too: Exponential function - practical use of geometric progression
solved exercises
Question 1 - A particular culture of bacteria is being observed for a few days by scientists. One of them is analyzing the growth of this population, and he noticed that, on the first day, there were 100 bacteria; in the second, 300 bacteria; in the third, 900 bacteria, and so on. Analyzing this sequence, we can say that it is:
A) an arithmetic progression of ratio 200.
B) a geometric progression of ratio 200.
C) an arimetic progression of reason 3.
D) a geometric progression of ratio 3.
E) a sequence, but not a progression.
Resolution
Alternative D.
Analyzing the sequence, we have the terms:
Note that 900/300 = 3, as well as 300/100 = 3. Therefore, we are working with a PG of ratio 3, as we are multiplying by three from the first term.
Question 2 - (Enem – PPL) For a beginner in running, the following daily training plan was stipulated: run 300 meters on the first day and increase 200 meters per day from the second. To count his performance, he will use a chip, attached to his sneaker, to measure the distance covered in training. Consider that this chip stores, in its memory, a maximum of 9.5 km of run/walk, and must be placed at the beginning of the training and discarded after exhausting the space for data reserve. If this athlete uses the chip from the first day of training, for how many consecutive days will this chip be able to store the mileage of that daily training plan?
A) 7
B) 8
C) 9
D) 12
E) 13
Resolution
Alternative B.
Analyzing the situation, we know that we have a PA with a reason of 200 and an initial ending equal to 300.
Furthermore, we know that the sum Sno = 9.5 km = 9500 meters.
With these data, let's find the term ano, which is the number of kilometers recorded on the last day of storage.
It is also worth remembering that any term ano can be written as:
Theno = the1 + (n - 1)r

Given the equation 200n² + 400n – 19000 = 0, we can divide all terms by 200, simplifying the equation and finding: n² + 2n – 95 = 0.
For delta and Bhaskara, we have to:
a = 1
b = 2
c = -95
Δ = b² - 4ac
Δ = 2² – 4 · 1 · (-95)
Δ = 4 – 4 · (-95)
Δ = 4 + 380
Δ = 384
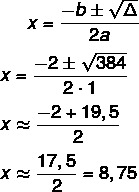
We know that 8.75 corresponds to 8 days and a few hours. In this case, the number of days in which the measurement can be performed is 8.
By Raul Rodrigues de Oliveira
Maths teacher
Source: Brazil School - https://brasilescola.uol.com.br/matematica/progressoes.htm

