The linear system consists of the mutual relationship between two or more equations, that is, equations that share the same solution or the same solution set. With this fact come the classifications regarding the sets, which are: Determined Possible System (only one solution), Undetermined Possible System (several solutions), Impossible System (none solution). However, we may come across equations whose coefficients are unknown, indeterminate parameters. Thus, through the discussion of the system, we can analyze these parameters and determine for which values will have Determined Possible Systems, or Indeterminate Possible Systems or Systems Impossible.
There is a matrix product that represents any linear system; therefore, we will analyze and classify the linear system according to the determinant of the matrix of coefficients of the equations. You must be asking yourself: "How so?" Therefore, see below the matrices that represent a 2x2 system (2 equations and 2 unknowns).
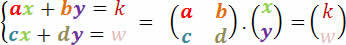
Therefore, our analysis will be based on the determinant of the coefficient matrix.

According to determinant D, we will have the following situations:

As mentioned, we can have these coefficients in the form of an unknown, and through this unknown, determine parameters for this determinant. Let's look at an example so that we can understand these terms.
1- Discuss the system, analyzing what the values are m and k.

We have to determine the value of the determinant D and analyze the parameters. So we have to:
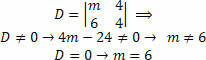
Thus, to obtain a possible and determined system, it is enough to have a value other than 6 for the coefficient (m).
However, if m is equal to 6 (m = 6), we will have D = 0, so we must determine what the classification of this system will be (SPI or SI).
Substituting for 6, we have:
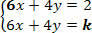
By scaling this system, we will obtain:
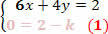
From equation (1) we can get two possibilities:
1) The value of k satisfies equation (1), that is: for k=2 we will have 0=0, and with this the system reduces only to the first equation, thus obtaining an Indeterminate Possible System (SPI).
2) If the value of k is different from 2, we will have a false equation, which will never be satisfied, such as (0 = 1), thus characterizing an Impossible System.
Therefore, discussing the system we have the following circumstances:
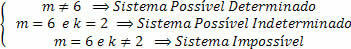
By Gabriel Alessandro de Oliveira
Graduated in Mathematics
Brazil School Team
Source: Brazil School - https://brasilescola.uol.com.br/matematica/discussao-analise-sistema-linear.htm
