We can list the binomial coefficients in a table called a Pascal triangle or Tartaglia. Remembering that we define the binomial coefficient using the following relation where n is over p and we indicate by: 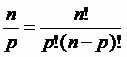
In Pascal's triangle we can observe the following situation: the coefficients with the same numerator (n) are in the same row and the denominator (p) in the same column. 
When we calculate the values of the coefficients we get a new representation for the triangle, see: 
On the same line, the numbers equidistant from the extremes are equal.
From the 2nd line we form the next one, just apply the Stifel relation, which says: each element is formed by the sum of two elements from the previous line. Watch: 
Sum of elements of each line 
Note that the elements of each line can be summed using a single power of base two and an exponent equal to the number of the line that you want to find the sum. Example:
The sum of the elements in line 9 is 29 = 512
by Mark Noah
Graduated in Mathematics
Brazil School Team
Newton's binomial - Math - Brazil School
Source: Brazil School - https://brasilescola.uol.com.br/matematica/propriedades-binomio-newton.htm
