You Prime numbers are part of the cardinal numbering system, which is composed of the natural numbers 0, 1, 2, 3, 4... The discovery of prime numbers took place in Alexandria, around 360 BC. C to 295 a. C, by the scholar Euclid. It was he who discovered that there are an infinite number of prime numbers and that any composite number can be decomposed into prime factors. Remember that a composite number is every natural number greater than one and that it has more than two natural numbers as a divisor. These are compound numbers: 4, 6. 8, 9, 10, 12.. .
The best known way to identify prime numbers is the Sieve of Eratosthenes, which is a practical algorithm used on numerical intervals. Eratosthenes was from Greece and lived in the period of 276 a. C to 194 a. C, was a great mathematician and was known to have calculated the Earth's circumference.
Numerical terms greater than 1, divisible by 1 and by itself are considered prime numbers. The number 1 is not prime, so the prime numbers are: 2, 3, 7, 11, 13, 17, 19, 23, 29, 31.. .
But how recognize prime numbers?
To identify a prime number we must successively divide it by prime numbers such as: 2, 3, 5... and check whether the division is exact (where the remainder is zero) or not exact (where the remainder is nonzero).
If the rest of the division for zero the number it's not cousin.
if no remainder for zero, the number is cousin.
To divide a number faster we can use the divisibility criteria, but only when the divisors are prime numbers, such as 2, 3, 5 and 11. Remember that:
A number is divisible by 2 when ending in even terms, ie 0, 2, 4, 6.. .
A number will be divisible by three when the sum of its digits is divisible by 3.
A number will be divisible by 5 when its last digit is 5 or 0.
A number will be divisible by 11 when the difference between the sum of the even-order digits and the sum of the odd-order digits yields a number divisible by 11.
When talking about the rest, we should always remember the division algorithm, which is given by:

See the following example:
Find out if the number 521 is prime.
To find out if the number 521 is prime we must check what the divisors of 521 are. We can do this using the divisibility criteria, that is, dividing 521 by the prime numbers: 2, 3, 5. We will stop dividing 521 by prime numbers when the quotient value is less than the divisor. If none of the remainder of the divisions is equal to zero, the number will be considered prime.
According to the divisibility criterion, 521 is not divisible by two because it is not an even number.
521 is not divisible by 3, because the sum of the digits that make it up is not divisible by 3. See 5 + 1 +1 = 7
The number 521 is also not divisible by 5, because the last digit of the number 521 is not 5.
521 is not divisible by 7, since seven is an inexact division and its remainder is 3.
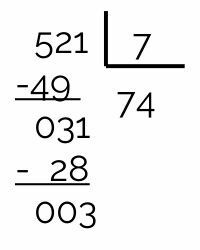
The number 11 is also not a divisor of 521, because its remainder is 4. Note that the quotient is greater than the divisor, so we should divide 521 by the next prime number, which is 13.
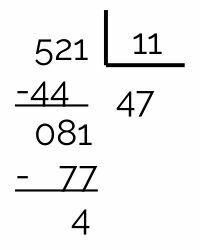
521 is not divisible by 13, because its division is not exact.

17 is not a divisor of 521, as the remainder of the division is 11. So we have to divide by the next prime number, which is 19.
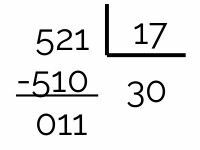
521 is not divisible by 19, because the rest of that division is 8.
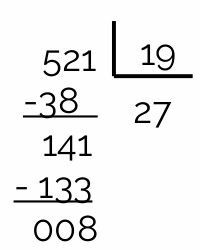
23 is not divisor of 521, the remainder of the division is 15. Since the quotient (22) is smaller than the divisor (23), we must stop dividing the number 521.
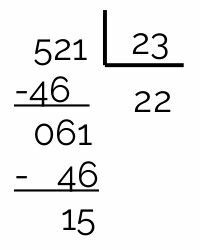
We conclude that 521 is a prime number, so it is divisible only by 1 and by itself (521).
By Naysa Oliveira
Graduated in Mathematics
Source: Brazil School - https://brasilescola.uol.com.br/matematica/como-reconhecer-os-numeros-primos.htm
