To determine the inverse matrix of a square matrix A of order n, it is enough to find a matrix B such that the multiplication between them results in an identity matrix of order n.
A*B = B*A = Ino
We say that B is the inverse of A and is represented by A-1.
Remember that the identity matrix of order n (In) is a matrix where the elements of its main diagonal are equal to 1 and the other elements are equal to 0. For example: 
Example 1
Given matrices A and B, check if one is the inverse of the other. 
Multiply the matrices and verify that the result consists of an identity matrix. 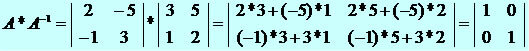
We can verify that A-1 it is the inverse of A, since the multiplication between them resulted in an identity matrix.
Example 2
Let's determine if the inverse matrix of A exists. 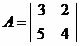
To determine the inverse of a matrix, simply multiply the matrix given by a generic matrix of terms a11, b12, c21, d22, given the equality of an identity matrix. Watch:
Solving systems: 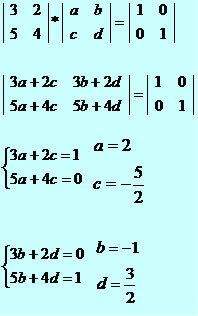
So, we have that the inverse matrix is: 
by Mark Noah
Graduated in Mathematics
Brazil School Team
Matrix and determinants - Math - Brazil School
Source: Brazil School - https://brasilescola.uol.com.br/matematica/existencia-uma-matriz-inversa.htm

