O set From whole numbers is made up of all numbers that are not decimal. In other words, the set of numberswhole is formed by the set of natural numbers and yours oppositesadditions. For example: the number 1 belongs to the set of natural numbers and whole numbers. The number – 1, on the other hand, belongs only to the set of whole numbers, as it is the additive opposite of the natural 1.
Elements of the whole number set
The elements of set From numberswhole are the natural numbers, their additive opposites, and zero. We highlight zero, as some authors do not consider it as numberNatural. Therefore, the elements of the whole number set are:
Z = {…, – 3, – 2, – 1, 0, 1, 2, 3, …}
The letter Z is used to represent the numbers. whole because this representation comes from the german Zahl, which means “number”.
You setsnumeric can be represented by the venn diagram. We will also use this representation to show that the set of numbersnatural is fully included in the set of numberswhole, that is, if a number is natural, then it is also an integer:
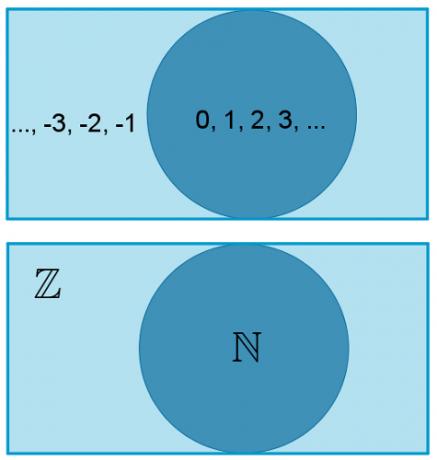
Note that all numberswhole are within the diagram and that non-negatives can be grouped. This grouping is the set of numbersnatural.
Subsets of Integers
It is possible to find, within the set of numberswhole, other subsets that are interesting, such as:
Z*: formed by all numberswhole, except for zero;
Z+: formed by all numberswhole not negative, that is, by the set of natural numbers itself. So, Z+ =N;
Z+*: formed by all numberswhole positive. So the number zero is not in this set. Its elements are: 1, 2, 3, 4, …;
Z–: formed by all numberswhole not positive, that is, by the additive opposites of the natural numbers and by zero;
Z–*: formed by all numberswhole negative. Thus, the number zero does not belong to this set.
Numerical line of whole numbers
You numberswhole can be placed on a straight. To do this, just mark the point where the zero number will be placed, called the origin, choose a measurement unit and use it to mark the whole numbers. The only rule for constructing this line is that the numbers be placed in ascending sequence, from right to left. For example: suppose the chosen unit of measure is the centimeter, the straightnumerical will look like the image below:
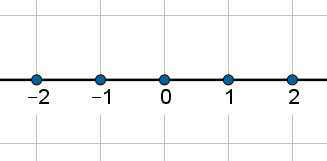
Note that starting at zero, the next number on the right is 1, then 2, and so on. To the left, the next number is – 1, then – 2, and so on. The distance between the number 1 and the number 2 is equal to 1 centimeter, as the distance between two consecutive numbers will always be equal to the unit of measure used. The distance between – 2 and 2 is 4 centimeters.
Note that a number on the right will always be greater than a number on the left. Because of this, we easily conclude that – 2 < 1.
modulus or absolute value
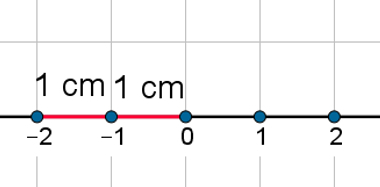
O module, or valueabsolute, on one numberwhole is the distance of this number to the origin of the straightnumerical. In other words, the modulus is the distance between zero and the observed number in the measurement unit in which the line was constructed. Since there are no negative distances, the modulus will always be a positive number. Also, the module of a number is represented by that number between two bars, as in: | – 2|.
Then the module of – 2 is the distance of that number to zero, so | – 2| = 2. Note this in the straightnumerical:
By Luiz Paulo Moreira
Graduated in Mathematics
Source: Brazil School - https://brasilescola.uol.com.br/o-que-e/matematica/o-que-e-conjunto-dos-numeros-inteiros.htm

