O Pythagorean theorem is one of right triangle metric relations, that is, it is an equality capable of relating the measures of the three sides of a triangle under these conditions. It is possible to discover, through this theorem, the measure of one side of a trianglerectangle knowing the other two measures. Because of this, there are several applications for the theorem in our reality.
Pythagoras theorem and the right triangle
One triangle is called rectangle when you have a angle straight. It is impossible for a triangle to have two right angles, because the sum of your internal angles is obligatorily equal to 180°. the side of this triangle which opposes the right angle is called hypotenuse. The other two sides are called peccaries.
Therefore, the Pythagorean theorem makes the following statement, valid for all trianglerectangle:
"The square of the hypotenuse is equal to the sum of the squares of the hips"
Mathematically, if the hypotenuse of the right triangle is "x" and the peccaries are "y" and "z", the theorem in Pythagoras guarantees that:
x2 = y2 + z2
Applications of the Pythagorean Theorem
1st Example
A land has a shape rectangular, so that one side is 30 meters and the other 40 meters. It will be necessary to build a fence that passes through the diagonal of that land. So, considering that each meter of fence will cost R$ 12.00, how much will be spent, in reais, for its construction?
Solution:
If the fence passes through diagonal of rectangle, then just calculate its length and multiply it by the value of each meter. To find the measure of the diagonal of a rectangle, we should note that this segment divides it into two. trianglesrectangles, as shown in the following figure:

Taking only the triangle ABD, AD is hypotenuse and BD and AB are peccaries. Therefore, we will have:
x2 = 302 + 402
x2 = 900 + 1600
x2 = 2500
x = √2500
x = 50
Thus, we know that the land will have 50 m of fence. As each meter will cost 12 reais, therefore:
50·12 = 600
R$ 600.00 will be spent on this fence.
2ºExample
(PM-SP/2014 – Vunesp). Two wooden stakes, perpendicular to the ground and of different heights, are 1.5 m apart. Another 1.7 m long stake will be placed between them, which will be supported at points A and B, as shown in the figure.
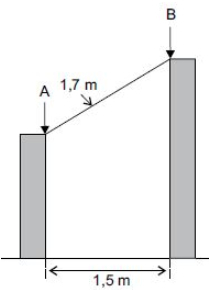
The difference between the height of the largest pile and the height of the smallest pile, in that order, in cm, is:
a) 95
b) 75
c) 85
d) 80
e) 90
Solution: The distance between the two piles is equal to 1.5 m, if measured at point A, forming the right triangle ABC, as indicated in the following figure:

Using the theorem in Pythagoras, we will have:
AB2 = AC2 + BC2
1,72 = 1,52 + BC2
1,72 = 1,52 + BC2
2.89 = 2.25 + BC2
BC2 = 2,89 – 2,25
BC2 = 0,64
BC = √0.64
BC = 0.8
The difference between the two stakes is equal to 0.8 m = 80 cm. Alternative D.
by Luiz Paulo
Graduated in Mathematics
Source: Brazil School - https://brasilescola.uol.com.br/matematica/aplicacoes-teorema-pitagoras.htm

