Radian is a unit of measurement used to measure angles and arcs of a circle, as well as degrees. They are used to represent the part of a circle of length equal to the radius, or a multiple of it.
The word radian refers to another, commonly used when thinking about circles: the radius. The radius element is a line segment that connects the center of a circle to any point on the line that determines it.
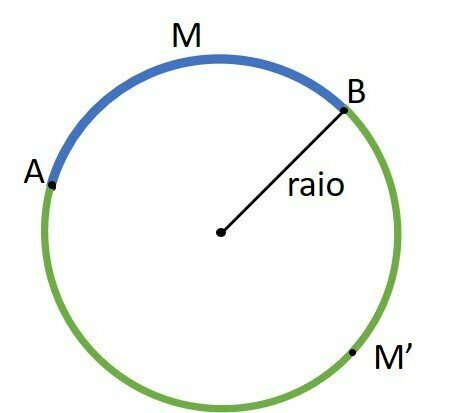
The highlighted curve between points A, M and B is the AMB arc. Repeat from points A and B determine two arcs, the blue AMB and the green AM'B. These arcs can be measured in radians or degrees.
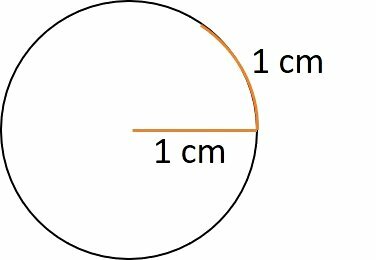
When determined by the central angle, the arc that has the same length as the radius has one radian.
1 radian is the measure of an arc equal to the radius of the circle.
The symbol for the radian unit of measurement is the rad.
Examples
An arc equal in length to the radius measures 1 rad.
An arc three times the length of the radius measures 3 rad.
An arc twenty-six times longer than the radius measures 26 rad.
Radians are widely used in mathematics. They provide measurements for circumference and trigonometry studies.
Radian to degree and degree to radian
As radian and degree are different measurement units, but used to measure the same quantity, it is common to relate them. It is important to know how to convert these measures.
Since antiquity, it has been experimentally observed that the arc of half a circumference divided by the length of the radius always results in the same number, approximately 3.141592... This number was called (pi).
As a half circle has 180º, we have:
= 180º
From this relation it is possible to transform any measure in radian to degree, as well as, degree into radian. For this, a rule of three is used.
Example 1
90 degrees represents what measure in radians
Setting up the proportion, we have:
Cross multiplying:
Example 2
3 rad equals how many degrees
You may be interested in:
- Trigonometric Circle
- Trigonometric Functions
- Angles: definition, types, how to measure and exercises
- PI number (π): value, origin, how to calculate and what it is for
ASTH, Rafael. Radian: what it is and how to measure it.All Matter, [n.d.]. Available in: https://www.todamateria.com.br/radiano-o-que-e-como-medir/. Access at:
See too
- Trigonometric Circle
- Trigonometry Exercises
- Trigonometry Exercises in the Right Triangle
- Angles
- 27 Basic Mathematics exercises
- Sine, Cosine and Tangent Exercises
- Exercises on uniform circular motion
- Pythagorean Theorem - Exercises