A identity matrix is a special kind of headquarters. We know as identity matrix In the square matrix of order n that has all terms on the diagonal equal to 1 and terms not belonging to the main diagonal equal to 0. The identity matrix is considered the neutral element of multiplication, that is, if we multiply a matrix M by the identity matrix, we find as a result the matrix itself M.
See too: What is the determinant of a matrix?
Topics of this article
- 1 - Summary about the identity matrix
-
2 - What is the identity matrix?
- ? Identity matrix types
- 3 - Properties of the identity matrix
- 4 - Multiplication of the identity matrix
- 5 - Solved exercises on identity matrix
Summary about identity matrix
The identity matrix is the square matrix with main diagonal elements equal to 1 and with the other elements equal to 0.
There are identity matrices of different orders. We represent the identity matrix of order n by I n.
The identity matrix is the neutral element of matrix multiplication, that is, \( A\cdot I_n=A.\)
The product of a square matrix and its inverse matrix is the identity matrix.
What is identity matrix?
The identity matrix is a special type of square matrix. A square matrix is known as an identity matrix if it has all elements on the main diagonal equal to 1 and all other elements equal to 0. Then, in every identity matrix:
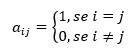
➝ Identity matrix types
There are identity matrices of different orders. the order n is represented by In. Let's see below some matrices of other orders.
Order 1 identity matrix:
\(I_1=\left[1\right]\)
Order 2 identity matrix:
\(I_2=\left[\begin{matrix}1&0\\0&1\\\end{matrix}\right]\)
Order 3 identity matrix:
\(I_3=\left[\begin{matrix}1&0&0\\0&1&0\\0&0&1\\\end{matrix}\right]\)
Order 4 identity matrix:
\(I_4=\left[\begin{matrix}1&0&0&0\\0&1&0&0\\0&0&1&0\\0&0&0&1\\\end{matrix}\right]\)
Order 5 identity matrix:
\(I_5=\left[\begin{matrix}1&0&0&0&0\\0&1&0&0&0\\0&0&1&0&0\\0&0&0&1&0\\0&0&0&0&1\\\end{matrix}\right]\)
Successively, we can write identity matrices of different orders.
Do not stop now... There's more after the publicity ;)
Identity matrix properties
The identity matrix has an important property, as it is the neutral element of the multiplication between the matrices. This means that any matrix multiplied by the identity matrix is equal to itself. Thus, given the matrix M of order n,we have:
\(I_n\cdot M=M\cdot I_n=M\)
Another important property of the identity matrix is that the product of a square matrix and its inverse matrix is the identity matrix. Given a square matrix M of order n, the product of M by its inverse is given by:
\(M\cdot M^{-1}=I_n\)
Read too: What is a triangular matrix?
Multiplication of the identity matrix
When we multiply a matrix M by the identity matrix of order n, we get the matrix M as a result. Let's see, below, an example of the product of the matrix M of order 2 by the identity matrix of order 2.
\(A\ =\ \left(\begin{matrix}a_{11}&a_{12}\\a_{21}&a_{22}\\\end{matrix}\right) \) It is \(I_n=\left(\begin{matrix}1&0\\0&1\\\end{matrix}\right)\)
Suposing that:
\(A\cdot I_n=B\)
We have:
\(B\ =\left(\begin{matrix}b_{11}&b_{12}\\b_{21}&b_{22}\\\end{matrix}\right)\)
So the product of A by \(I_n\) it will be:
\(b_{11}=1\cdot a_{11}\cdot1+0\cdot a_{12}=a_{11}\)
\(b_{12}=0\cdot a_{11}+1\cdot a_{12}=a_{12}\)
\(b_{21}=1\cdot a_{21}+0\cdot a_{22}=a_{21}\)
\(b_{22}=0\cdot a_{21}+1\cdot a_{22}=a_{22}\)
Note that the terms of matrix B are identical to the terms of matrix A, that is:
\(A\cdot I_n=\left[\begin{matrix}a_{11}&a_{12}\\a_{21}&a_{22}\\\end{matrix}\right]=A\)
Example:
Being M The matrix \(M=\ \left[\begin{matrix}1&4&0\\2&5&3\\-3\ &-2&1\\\end{matrix}\right]\), calculate the product between the matrix M and the matrix \(I_3\).
Resolution:
Carrying out the multiplication, we have:
\(M\cdot I_3=\left[\begin{matrix}1&4&0\\2&5&3\\-3\ &-2&1\\\end{matrix}\right]\cdot\left[\begin{matrix}1&0&0\\0&1&0\\0&0&1\\\end{matrix}\right]\)
\(M\cdot I_3=\left[\begin{matrix}1\ \cdot\ 1\ +\ 0\ \cdot\ 4\ +\ 0\ \cdot\ 0&1\cdot0\ +\ 4\ \cdot\ 1\ +\ 0\cdot\ 0&1\cdot0+4\cdot0+0\cdot1\\2\cdot\ 1\ +\ 5\ \cdot\ 0\ +\ 3\ \cdot\ 0&2\ \cdot\ 0\ +\ 5\cdot1+3\cdot0&2\cdot0+5\cdot0+3\cdot1\\-3\cdot1+\left(-2\right)\cdot0+1\cdot0&-3\cdot0+\left(-2\right)\cdot1+1\cdot0&-3\cdot0+\left(-2\right)\cdot0+1\cdot 1\\\end{matrix}\right]\)
\(M\cdot I_3=\left[\begin{matrix}1&4&0\\2&5&3\\-3\ &-2&1\\\end{matrix}\right]\)
Solved exercises on identity matrix
question 1
There is a square matrix of order 3 which is defined by \(a_{ij}=1 \) when \(i=j\) It is \(a_{ij}=0\) It is when \(i\neq j\). This matrix is like:
A) \( \left[\begin{matrix}1&1&1\\1&1&1\\1&1&1\\\end{matrix}\right]\)
B) \( \left[\begin{matrix}0&0&1\\0&1&0\\1&0&0\\\end{matrix}\right]\)
W) \( \left[\begin{matrix}0&1&1\\0&0&1\\0&0&1\\\end{matrix}\right]\)
D) \( \left[\begin{matrix}1&0&0\\0&1&0\\0&0&1\\\end{matrix}\right]\)
AND) \( \left[\begin{matrix}1&0&0\\1&1&0\\1&1&1\\\end{matrix}\right]\)
Resolution:
Alternative D
Analyzing the matrix, we have:
\(a_{12}=a_{13}=a_{21}=a_{23}=a_{31}=a_{32}=0\)
\(a_{11}=a_{22}=a_{33}=1\)
So, the matrix is equal to:
\(\left[\begin{matrix}1&0&0\\0&1&0\\0&0&1\\\end{matrix}\right]\)
question 2
(UEMG) If the inverse matrix of \(A=\left[\begin{matrix}2&3\\3&x\\\end{matrix}\right]\) é \( \left[\begin{matrix}5&-3\\-3&2\\\end{matrix}\right]\), the value of x is:
A) 5
B) 6
C) 7
D) 9
Resolution:
Alternative A
Multiplying the matrices, we realize that their product is equal to the identity matrix. Calculating the product of the second row of the matrix by the first column of its inverse, we have:
\(3\cdot5+x\cdot\left(-3\right)=0\)
\(15-3x=0\)
\(-\ 3x=0-15\ \)
\(-\ 3x=-\ 15\)
\(x=\frac{-15}{-3}\)
\(x=5\ \)
By Raul Rodrigues de Oliveira
Maths teacher
Would you like to reference this text in a school or academic work? Look:
OLIVEIRA, Raul Rodrigues de. "Identity matrix"; Brazil School. Available in: https://brasilescola.uol.com.br/matematica/matriz-identidade.htm. Accessed on July 20, 2023.
Understanding the application of matrices is an important fact in order not to be left behind in the entrance exam. The application of the matrices in the entrance exams is carried out by relating several of the concepts of matrices in just one question.
Learn how to calculate the determinants of square matrices of order 1, 2, and 3. Learn how to use Sarrus' rule. Know the properties of determinants.
Understand here the definitions and formalizations of the matrix structure. See also how to operate its elements and the different types of matrices.
Click here and learn what a symmetric matrix is. Know its properties and discover how it differs from an antisymmetric matrix.
Understand what a transpose matrix is. Know the properties of a transposed matrix. Learn how to find the transposed matrix of a given matrix.
Learn to calculate the multiplication between two matrices, as well as know what the identity matrix is and what the inverse matrix is.
Know Cramer's rule. Learn to use Cramer's rule to find solutions to a linear system. See worked examples of Cramer's rule.
Do you know the Sarrus Rule? Learn how to use this method to find the determinant of 3x3 matrices.
Cringe
The slang adapted from English is used to designate someone who is seen as tacky, shameful, outdated and out of fashion.
Neurodiversity
A term coined by Judy Singer, it is used to describe the wide variety of ways the human mind behaves.
PL of Fake News
Also known as PL2660, it is a bill that establishes mechanisms for the regulation of social networks in Brazil.