The area of a convex polygon is the space filled by its surface. Every time we obtain the calculation of the area of a certain region, its measurement unit will be squared (km², cm², m² etc.).
O trapeze it is a quadrilateral, given that it has four sides. The sum of its internal and external angles equals 360°. Every trapeze has a pair of parallel sides. Look at the figure below:

To calculate the area of a trapezoid, we must know the measurements referring to the major base (b), minor base (a) and height (h). Look:

♦ Trapezium area formula
The formula we use to calculate the trapeze area is as follows:
A = ½. h (a + b)
A = Trapezium area.
h = height.
a = base smaller.
b = larger base
Let's solve two examples to learn how to use the trapeze area formula.
♦ Trapezium area calculation examples
Example 1
Calculate the area of the trapeze below:
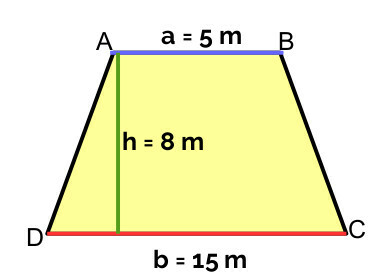
A = ½. H. (a + b)
A = ½. 8. (5 + 15)
A = ½. 8. (20)
A = ½. 160
A = 160/2
H = 80 m2
Example 2
The trapeze is one of the polygons used in making mosaics.

Suppose that one of the red tiles in the mosaic has the following measurements: Larger base: 4 cm, smaller base 2 cm, and 2.5 cm height. Calculate the area of this piece of the mosaic.
b = 4 cm
a = 2 cm
h = 2.5 cm
A = ½. H. (a + b)
A = ½. 2.5 cm. (4 cm + 2 cm)
A = ½. 2.5 cm. (6 cm)
A = ½. 15 cm2
A = 15 cm2
2
H = 7.5 cm2
By Naysa Oliveira
Graduated in Mathematics
Source: Brazil School - https://brasilescola.uol.com.br/matematica/area-trapezio.htm
