A area of squareis the measure of its surface and can be calculated by squaring its side. A square is a quadrilateral that has all congruent sides, that is, with the same measure, which makes it a particular case of quadrilateral.
as in rectangles, the area of the square is equal to the product of its base and its height, but as in the square a base and height are congruent, so we can calculate its area by raising the length of the side to the square.
Read too: Area of right triangle — how to calculate?
Topics of this article
- 1 - Summary of square area
- 2 - What is a square?
- 3 - What is the formula for the area of the square?
- 4 - How to calculate the area of the square?
- 5 - Differences between the area and perimeter of the square
- 6 - Diagonal of the square
- 7 - Solved exercises on square area
Square area summary
- A square is a polygon that has 4 sides of the same length.
- The area of the square is calculated by squaring the side length.
- Given a square of side l, its area is given by the following formula:
\(A=l^2\)
- In addition to the area of the square, we can also calculate the perimeter and diagonal of the square, measurements that are just as important as the area.
- Given a square of side l, its perimeter is given by the following formula:
\(P=4l\)
- Given a square of side l, the length of the diagonal is given by the following formula:
\(d=l\sqrt2\)
Do not stop now... There's more after the publicity ;)
What is a square?
The square is a case of polygon, classified as quadrilateral, because it has 4 sides, and like a regular polygon, because it has all congruent sides, that is, the square is a quadrilateral with all sides the same length.
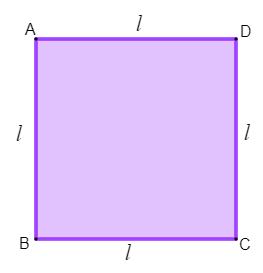
What is the formula for the area of the square?
A area is the surface area of a plane figure. To calculate the area of the square, we use the following formula:
\(A=l^2\)
How to calculate the area of the square?
We multiply the length of its base by its height. Since, in a square, the base and the height have the same measure, the area of the square can be calculated by the square of the side. Thus, to calculate the area of the square, knowing the length of its side, just square the side length, as it has congruent sides and would be the same thing as multiplying the length of its base by its height.
- Example:
What is the area of a square that has sides measuring 6 cm?
Resolution:
The area of this square with l = 6 é:
\(A=l^2\)
\(A=6^2\)
\(A=36\)
The area of this square is 36 cm².
- Example 2:
Calculate the area of the following square:
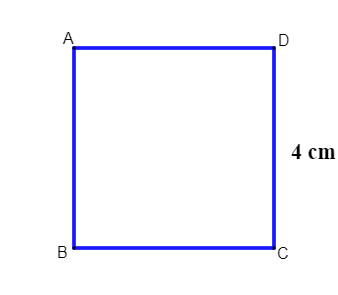
Resolution:
We know that the side of this square is 4 cm, so its area will be:
\(A=l^2\)
\(A=4^2\)
\(A=16\)
The area is 16 cm².
Differences between area and perimeter of square
Area and perimeter are two important measurements of any polygon, and they represent different quantities. Generally, the area is the measure of the surface of the polygon, that is, it is the measure of the internal region of the plane figure. The measurement of the area always has two dimensions, and therefore we have the square meter as the unit of measurement of the area, and its multiples and submultiples.
The perimeter of a plane figure is another important quantity, being the contour of the figure. We can calculate the perimeter of a polygon by adding the length of its sides, and, unlike the area, the perimeter has only one dimension, its unit is the meter, with its multiples and its submultiples.
- Example:
A square has sides measuring 5 meters, so what is the area and perimeter of this square?
Resolution:
Starting with the area, we have:
\(A=l^2\)
\(A=5^2\)
\(A=25\ \)
We know that the area is given in square units, so the area is 25 m².
Now we will calculate the perimeter. As the square has 4 congruent sides, the perimeter of the square is equal to the sum of the measures of its four sides, that is, P = 4l. Calculating the perimeter, we have:
\(P=4l\)
\(P=4\cdot5\)
\(P=20\m\)
square diagonal
Knowing the measure of the side of the square, another important measure that we can identify in the square is the diagonal. The diagonal of the square and the line segment that connects two non-consecutive vertices of the square.

To calculate the length of the diagonal, we use the formula:
\(d=l\sqrt2\)
Knowing that \(\sqrt2\) it is a irrational number, we can indicate the value of the side times \(\sqrt2\), or, if necessary, use an approximation for the value of \(\sqrt2\).
- Example:
What is the length of the diagonal of a square whose side is 3 cm?
Resolution:
A square has a side of 3 cm, so its diagonal will measure \( 3\sqrt2\) cm. If we want an approximation, for example, using \(\sqrt2=1,4\), we will consider that the measure of this diagonal will be \(3\cdot1,4=4.2\ cm\).
See too: Circle area — how to calculate?
Solved exercises on square area
question 1
A plot of land in the shape of a square has an area of 324 m². So we can say that the length of the side of this land is:
A) 15 meters
B) 16 meters
C) 17 meters
D) 18 meters
E) 19 meters
Resolution:
Alternative D
We know that the area is equal to the square of the side length:
\(A=l^2\)
As we know that the area is 324 m², then we have:
\(l^2=324\)
\(l=\sqrt{324}\)
\(l=18\ \)
The measurement of the side of this land will be 18 meters.
question 2
On a square piece of land, with sides measuring 8 meters, a swimming pool will be placed, also square, with sides measuring 3 meters. The remainder of this land will be grass. So the area to be grassed measures:
A) 9 m²
B) 25 m²
C) 36 m²
D) 55 m²
E) 64 m²
Resolution:
Alternative D
We will calculate the difference between the land and pool areas, starting with the land area:
\(A_{terrain}=8^2\)
\(A_{terrain}=64\ m^2\)
Now calculating the pool:
\(A_{swimming pool}=3^2\)
\(A_{swimming pool}=9\ m^2\ \)
The difference between them is 64 – 9 = 55 m².
By Raul Rodrigues de Oliveira
Maths teacher
Learn to classify a polygon according to the number of sides. Also differentiate a convex polygon from a non-convex one and a regular one from an irregular one.
Learn the definition of a parallelogram and its properties, as well as learn about the main parallelograms and their formulas for area and perimeter.
Learn what a regular polygon is and differentiate regular polygons from irregular polygons. Also, calculate the area and perimeter of a regular polygon.
Learn what polygons are and what their elements are. Know the method of naming polygons and how we add the internal and external angles.
Get to know quadrilaterals and the basic characteristics that lead them to be classified as parallelograms, trapezoids or neither.
Know the characteristics of the rectangle. Calculate the area, perimeter and diagonal length of a rectangle. Understand the main properties of this polygon.