O cube volume is the space that this geometric solid occupies. The cube, also known as hexahedron, is the geometric solid composed of 6 square faces. Therefore, the volume of the cube depends only on the measure of its edge. The volume of the cube is equal to the length of the edge to the power of 3, that is, V = The³.
See too: Cylinder volume — how to calculate?
Topics in this article
- 1 - What is the formula for the volume of the cube?
- 2 - How to calculate the volume of the cube?
- 3 - Volume measurement units
- 4 - Solved exercises on cube volume
What is the formula for the volume of the cube?
To understand the formula for the volume of the cube, we will remember its main features. The cube is a special case of polyhedron. It consists of 6 square faces, 12 edges and 8 vertices. In the cube, all edges are congruent. In addition to being a polyhedron, the cube is considered a paving stone, since all its faces are formed by squares. See the image below.
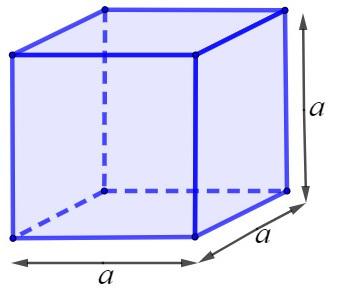
The volume of the cube is the multiplication length by height and width. As all its edges are congruent, measuring
The, the volume of the cube is nothing more than the cube of the edge, that is:\(V=a^3\)
Do not stop now... There's more after the ad ;)
How to calculate the volume of the cube?
To calculate the volume of the cube, knowing the length of its edge, just calculate the cube of the edge.
Example:
A container is shaped like a cube with an edge of 12 centimeters, so the volume of the cube is:
Resolution:
V = The³
V = 12³
V = 1728 cm³
The volume of this container is 1728 cm³.
Example 2
A polyhedron has 6 faces, all square, with edges measuring 4 meters, so the volume of this polyhedron is:
Resolution:
We can see that this polyhedron is a cube, so just calculate the volume of the cube:
V = a³
V = 4³
V = 64 m³
Read too: Cone volume — how to calculate?
Volume measurement units
Volume is the space that a given body occupies and has cubic meters (m³) as its fundamental unit. In addition to cubic meters, there are submultiples and multiples of this unit of measurement.
The submultiples are:
cubic millimeter: mm³
cubic centimeter: cm³
cubic decimeter: dm³
The multiples are:
cubic dekameter: dam³
cubic hectometer: hm³
cubic kilometer: km³
We can also relate the measure of volume to the measure of capacity, which is measured in liters. In general, we have:
1 m³ = 1000 l
1 dm³ = 1 l
1 cm³ = 1 ml
Cube volume solved exercises
question 1
(Enem 2010) A wooden pencil holder was built in the cubic format, following the model illustrated below. The cube inside is empty. The edge of the larger cube measures 12 cm, and that of the smaller cube, which is internal, measures 8 cm.
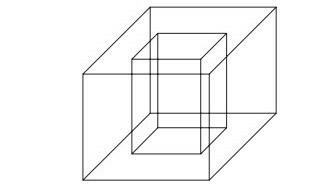
The volume of wood used in the manufacture of this object was
A) 12 cm³
B) 64 cm³
C) 96 cm³
D) 1216 cm³
E) 1728 cm³
Resolution:
Alternative D
To calculate the volume of wood, we will calculate the difference between the volume of the larger cube and the volume of the smaller cube.
The smaller cube has an edge measuring 8 cm:
\(V_1=8^3\)
\(V_1=512\)
The largest cube has an edge measuring 12 cm:
\(V_2={12}^3\)
\(V_2=1728\)
Calculating the difference between them, it is concluded that the volume of wood used was:
\(V=V_2-V_1\)
\(V=1728-512\)
\(V=1216\ cm^3\)
question 2
(Vunesp 2011) A company's products are packed in cubic boxes, with an edge of 20 cm. For transport, these packages are grouped together, forming a rectangular block, as shown in the figure. It is known that 60 of these blocks completely fill the cargo compartment of the vehicle used for their transport.

It can be concluded, then, that the maximum volume, in cubic meters, transported by this vehicle is:
A) 4.96.
B) 5.76.
C) 7.25.
D) 8.76.
E) 9.60.
Resolution:
Alternative B
First, we will calculate the volume of a cube. Knowing that its edge is 20 cm and transforming this value into meters, we have 0.2 m of edge.
\(V_{cube}={0.2}^3\)
\(V_{cube}=0.008\ m^3\)
From the image you can see that each rectangular block has 12 cubes, so the volume of the block will be:
\(V_{block}=12\cdot0.008\)
\(V_{block}=0.096\ m^3\)
Finally, we know that 60 blocks can fit in the transport vehicle, so the maximum load volume is:
\(V_{maximum}=0.096⋅60=5.76 m^3\)
By Raul Rodrigues de Oliveira
Maths teacher
Would you like to reference this text in a school or academic work? Look:
OLIVEIRA, Raul Rodrigues de. "Cube volume"; Brazil School. Available in: https://brasilescola.uol.com.br/matematica/volume-do-cubo.htm. Accessed on July 24, 2022.


