Exercises on division and multiplication of fractions

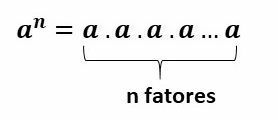
Practice multiplication and division of fractions with the template exercises. Clear your doubts with the step-by-step commented resolutions.

Exercise 1

Multiply the fractions 3 over 5 space and space 7 over 4 .

see answer

Answer: 21/20

To multiply fractions, we multiply numerator by numerator and denominator by denominator.

$3 over 5 space multiplication sign space 7 over 4 equals numerator 3 multiplication sign 7 over denominator 5 multiplication sign 4 end of fraction equals 21 over 20$

Exercise 2

divide the fractions $numerator 15 over denominator 3 space end of fraction space and space 12 over 8$ .

see answer

Answer: 120/36

To divide fractions, we repeat the first and multiply by the inverse of the second. Inverting the fraction means swapping the denominator and numerator.

$numerator 15 over denominator 3 space end of fraction space divided by space 12 over 8 equals numerator 15 over denominator 3 space end of fraction space multiplication sign space 8 over 12 equals 120 over 36$

Exercise 3

solve the expression 9 over 5 space multiplication sign space 4 over 3 space divided by space 12 over 15 .

see answer

Answer: 540/180

9 over 5 space multiplication sign space 4 over 3 space divided by space 12 over 15 equals 36 over 15 divided by space 12 over 15 equals 36 over 15 multiplication sign space 15 over 12 equals 540 over 180

Exercise 4

calculate $numerator start style show 2 over 4 end of space style multiplication sign space start style show 4 over 1 end of style over denominator start style show 7 over 14 end of style divided by start style show 1 middle end of style end of fraction$ .

see answer

Answer: 2

$numerator start style show 2 over 4 space multiplication sign space 4 over 1 end of style over denominator start style show 7 over 14 divided by 1 half style end fraction end equals numerator start style show numerator 2 space. space 4 over denominator 4 space. space 1 end of fraction space end of style over denominator start style show numerator 7 space. space 2 over denominator 14 space. space 1 end of fraction end of style end of fraction equal to numerator start style show 8 over 4 space end of style over denominator start style show 14 over 14 end of style end of fraction equals 2 over 1 equals at 2$

Exercise 5

Calculate: $numerator opens parentheses start style show 48 over 25 end of style divided by start style show 5 over 12 end of style close parentheses multiplication sign open parentheses start style show 4 over 9 end of style divided by start style show 8 over 3 end of style closes parentheses over denominator start style show 5 over 3 end of style divided by start style show 8 over 9 end of style end of fraction$

see answer

Answer: 768/1875

$start style math size 16px numerator open parentheses start style show 48 over 25 divided by 5 over 12 style end close parentheses multiplication sign open parentheses start style show 4 over 9 divided by 8 over 3 end style close parentheses over denominator start style show 5 over 3 divided by 8 over 9 end style end from fraction equals numerator open parentheses start style show 48 over 25 multiplication sign 12 over 5 end style close parentheses multiplication sign open parentheses start style show 4 over 9 multiplication sign 3 over 8 end of style close parentheses over denominator start style show 5 over 3 multiplication sign 9 over 8 end of style end of fraction equals numerator 576 over 125 multiplication sign 12 over 72 over denominator start style show 45 over 24 end of style end of fraction equal to numerator start style show 6912 over 9000 end of style over denominator start style show 45 over 24 end of style end of fraction equals 6912 over 9000 multiplication sign 24 over 45 equal to end of style$

At this point, you can simplify the expression to make the calculation easier.

$start style math size 16px numerator 6 space 912 divided by 3 over denominator 9 space 000 divided by 24 end of fraction multiplication sign numerator 24 divided by 24 over denominator 45 divided by 3 end of fraction equals numerator 2 space 304 over denominator 375 end of fraction multiplication sign 1 over 15 equals end of style$

Again, it is possible to simplify.

$start style math size 16px numerator 2 space 304 divided by 3 over denominator 375 end of fraction multiplication sign numerator 1 over denominator 15 divided by 3 end of fraction equals 768 over 375 multiplication sign 1 fifth equals 768 over 1875 end of style$

Exercise 6

The quarter of a number divided by 7/3 is equal to 9/8. What number is this?

see answer

Answer: 63/24

$numerator start style show x over 4 end of style over denominator start style show 7 over 3 end of style end of fraction equals 9 over 8 x over 4 multiplication sign 3 over 7 equals 9 over 8 numerator 3 x over denominator 28 end of fraction equals 9 over 8 3 x space equals numerator space 9 space multiplication sign 28 over denominator 8 end of fraction 3 x space equals 252 over 8 x space equals space numerator 252 over denominator 8 space multiplication sign space 3 end of fraction x space equals space 252 over 24$

Exercise 7

A survey carried out with students at a college found that 3/4 play sports. Of these, 2/6 play basketball. If the survey was conducted with 60 students, how many play basketball?

instagram story viewer

see answer

Answer: 15 students play basketball.

First we define how many students practice sport.

3 over 4 d and space 60 equals 3 over 4 multiplication sign space 60 equals 3 over 4 multiplication sign space 60 over 1 equals 180 over 4 equals 180 divided by 4 equals 45

45 students play sports, of these, 2/6 play basketball. Now we define the number of students who play basketball.

2 over 6 space d e space 45 space equals space 2 over 6 space multiplication sign space 45 space equals 2 over 6 space multiplication sign space 45 over 1 space equals 90 over 6 equals 15

Thus, 15 students play basketball.

Exercise 8

A new soda industry has just launched 2/5 and 3/4 liter cans. In its reservoirs there are 5,400 liters ready to be filled and sold. With which of the two can options will there be more units of the product? What is the difference between the number of units in the two can options?

see answer

Answer: 2 160 units with 2/5 cans and 4 050 units with 3/4 cans. The difference is 1 890 units.

Calculation for the 2/5 liter reservoir:

$2 over 5 d e space 5 space 400 space equals space 2 over 5 multiplication sign numerator space 5 space 400 over denominator 1 end of fraction space equals numerator 10 space 800 over denominator 5 end of fraction equals 2 space 160$

2160 units will be filled with 2/5 liter cans.

Calculation for the 3/4 liter reservoir:

$3 over 4 d e space 5 space 400 space equals space 3 over 4 multiplication sign numerator space 5 space 400 over denominator 1 end of fraction space equals numerator 16 space 200 over denominator 4 end of fraction equals 4 space 050$

4,050 units will be filled with 3/4 liter cans.

To calculate the difference between the quantities, we do:

4 050 - 2 160 = 1 890

Exercise 9

At a business presentation, coffee will be served in cups with a capacity of 2/40 of a liter. There are 43 participants, five of whom warned that they do not drink coffee. If a bottle of coffee has a capacity of 3/4 of a liter and each participant will be served a cup, how many bottles, at least, will be needed to serve the participants?

see answer

Answer: At least 2.5 bottles of coffee.

The number of people who will drink coffee is:

43 - 5 = 38

The total amount of coffee served will be:

38 space multiplication sign 2 over 40 equals 76 over 40

Dividing the total amount of coffee by the capacity of each bottle, we will have:

76 over 40 divided by 3 over 4 equals 76 over 40 multiplication sign 4 over 3 equals 304 over 120

Dividing the numerator by the denominator:

304 space divided by space 120 space approximately equal space 2 comma 5333 space...

We concluded that to serve all participants it will be necessary to prepare a little more than two and a half bottles of coffee.

Exercise 10

(Enem 2015 modified) Alcohol used as automotive fuel (hydrated ethanol) must have a maximum rate of water in its composition so as not to harm the engine's operation. A simple and quick way to estimate the amount of ethanol in a mixture with water is to measure the density of the mixture. The graph shows the variation of the density of the mixture (water and ethanol) with the percentage fraction of the mass of ethanol (fe), given by the expression

$f with e subscript equals 100 space multiplication sign numerator m with e subscript over denominator m with e subscript space plus space m with a subscript end of fraction$

where me and ma are the masses of ethanol and water in the mixture, respectively, at a temperature of 20 °C.

Image associated with the resolution of the issue.

Available at: www.handymath.com. Accessed on: 8 Aug. 2012.

Suppose that in a routine inspection carried out at a certain station, it was found that 50.0 c m cubed of fuel alcohol have a mass of 45.0 g. What is the percentage fraction of ethanol in this mixture? What is the proportional relationship between the mass of water and ethanol present in the fuel sample?

see answer

Answer: fe = 55; ma = 0.81m and.

The graph gives the change in density with the change in percent fraction fe.

Density is calculated by dividing mass by volume.

rho space equals space 45 over 50 equals 0 comma 9 space g divided by cm cubed

Following the line of density 0.9 g/cm³ horizontally, we cross with f equal to 55. Thus, the percentage fraction of ethanol in this mixture is 55.

Using the formula, substituting the values and solving for ma, we have:

$f with e subscript equals 100 space multiplication sign numerator m with e subscript over denominator m with e subscript space plus space m with a subscript end of fraction f with e subscript left parenthesis m with e subscript space plus space m with a subscript right parenthesis equals 100 m with e subscribed$