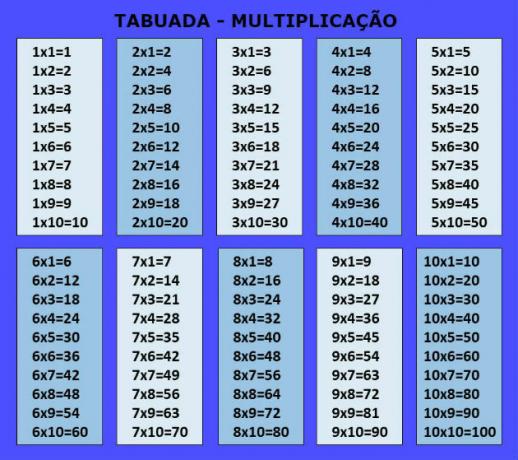
Complete multiplication tables: how to learn multiplication tables

The best way to know your multiplication tables is to understand your process. Previously, it was essential to memorize the multiplication table at school, however, nowadays the method to learn the multiplication table has gone from mere repetition to understanding how it works.

For this reason, there are now many games and exercises that make it easier to memorize the results of the times tables.

Multiplication Table

Among the types of times tables, the most important is that of multiplication. It displays the product between the numbers. In the image below we have the tables from 1 to 10:

If we want to know what 9 x 5 is worth, we can arrive at the result by adding. That is, 9 + 9 + 9 + 9 + 9 = 45.

Thus, we must take into account that multiplication corresponds to the sum of equal parts.

Starting with the simplest times tables, for example 2, 5, and 10, can be a good way to learn to memorize times tables.

One way to know the table of nine is to perform this count by joining the previous number of what is being multiplied, with the other number that is missing to reach nine.

instagram story viewer

Example: 9 x 7 = 63 (because 6 comes before 7 and 3 is missing to reach 9).

Another alternative to the 9 times tables is to use your fingers and move each finger from left to right. So if we want to know how much 9 x 7 is, we have to lower the seventh finger from left to right. On one side are 6 and on the other 3, which results in 63.

Likewise, if we want to know how much is 3 x 9, we lower the third finger and we have: 2 on one side and 7 on the other: 27.

Note: Remember that every number multiplied by zero (0) is always zero, eg 0 x 5 = 0. Also, every number multiplied by 1 will be itself, for example: 1 x 4 = 4.

Division Table

The division table also helps in mathematical calculations, since through this operation, we can find the results of the multiplication table. This is because the multiples and divisors of a number are related.

Example:

8 x 4 = 32 (multiplication table)
32: 8 = 4 (table of division)

Check the division tables below:

See too: Division and Division Exercises

Addition Times Table

Through the addition table, we can perform various calculations in mathematics. Look at the image below:

Subtraction Table

In addition to the addition times tables, we have the subtraction times tables:

Remember that by adding and subtracting numbers, we can better memorize and understand the relationship between them.

How to learn times tables: Cartesian times tables

Another way to write the result of multiplying numbers is through the Cartesian table. Unlike the most common times tables, it is constructed by placing numbers vertically and horizontally.

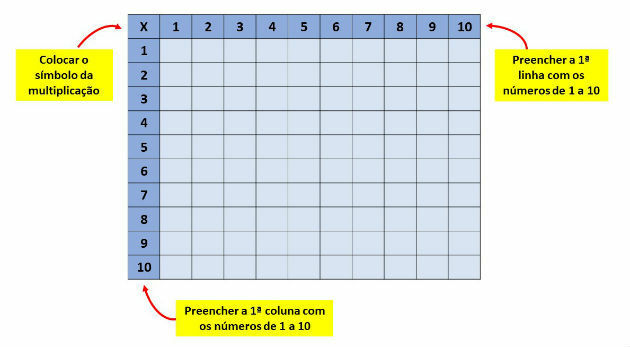
Let's now learn how to build the Cartesian times tables. First draw a big square with 11 rows and 11 columns.

In the first square of the first row, let's put X and write the numbers from 1 to 10 in each square of this row. Repeat the same for the first column.

At this point, our times tables will be as shown below:

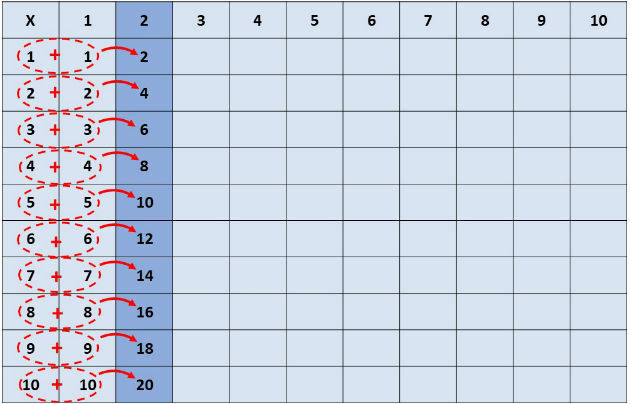
Building the Cartesian multiplication table

In the second column we will write the table of 1. To do this, just write the numbers 1 to 10. Since 1 is the neutral element of multiplication, any number multiplied by 1 is itself.

In the third column, we will fill in the table of 2. For this, you can add the two numbers that are written on the same line, as indicated in the figure:

In the fourth column we will write the multiplication table of 3. We can proceed in the same way as we did to write the tables of 2, that is, add the two previous values that are on the same line.

We note that 4 equals 2x2. Thus, we can write in the column of the tables of 4 the result of the values of the tables of 2 multiplied by 2.

To write the times tables of 5, we can add the result of the times tables of 2 with the result of the times tables of 3, since 2+3 = 5.

We observe that 6 is equal to 2x3, so let's put the result of the times tables of 3 multiplied by 2 in the column referring to the times tables of 6, as shown in the figure below.

We can also find the values related to the tables of 7, adding both the values of the tables of 2 and the table of 5 (2 + 5 = 7), the table of 3 with that of 4 (3 + 4 = 7), or even the table of 6 with that of 1 (6 + 1 = 7).

For the 8 times tables, we can either add the times tables where the numbers add up to 8 (1 with 7, 2 with 6 and 3 with 5), or use the fact that 8 is equal to 2 x 4.

In the table of 9 we can use the sum of the numbers that add up to 9, or we can fill the table using the following trick: complete the column from top to bottom, with the numbers from 0 to 9, then do the same thing, but placing the numbers, starting from 0, from bottom to up.

Finally, we complete the table with the table of 10. To do this, just put the numbers from 1 to 10 in the last column and then put the 0 at the end of each one of them.

Thus, we complete the Cartesian multiplication table. To find out the result of multiplying two numbers using this times tables, we must associate the numbers in the row with those in the column.

For example, if we want to find out how much is 7 x 9, just follow the column number 7 with the line number 9, where they meet is the result of the multiplication.

We represent in the figure below the tables from 1 to 10. Note that the numbers that are highlighted on the diagonal represent the perfect squares.

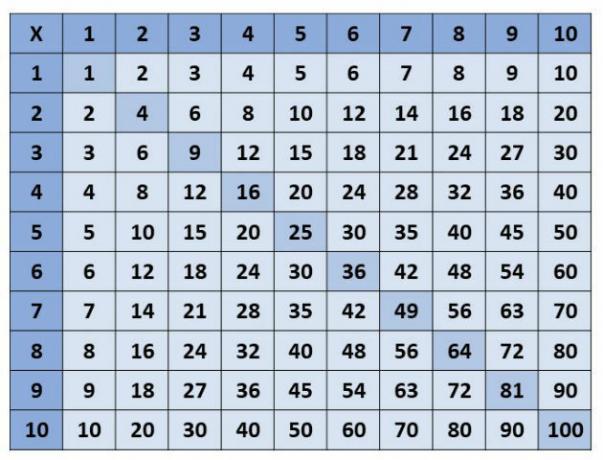
Looking at the table above, we notice that the diagonal with perfect squares divides the multiplication table into two parts, whose values are repeated symmetrically.

This is due to the fact that in multiplication the order of factors does not change the product, that is: 9 x 5 = 5 x 9. So you only need to memorize half of the multiplication tables from 1 to 10.