Hexagon it's the polygon which has 6 sides. It is regular when all sides and interior angles are congruent with each other. It is irregular when it does not have these characteristics. The first case is the most widely studied, because when the hexagon is regular, it has specific properties and formulas that allow us to calculate its area, perimeter and apothem.
Read too: What is a losangle?
Abstract about hexagon
Hexagon is a 6-sided polygon.
It is regular when all sides are congruent.
It is irregular when all sides are not congruent.
In a regular hexagon, each interior angle measures 120°.
The sum of angles outer edges of a regular hexagon is always 360°.
To calculate the area of a regular hexagon, we use the formula:
\(A=\frac{3L^2\sqrt3}{2}\)
O perimeter of a hexagon is the sum of its sides. When it is regular, we have:
P = 6L
The apothem of a regular hexagon is calculated by the formula:
\(a=\frac{\sqrt3}{2}L\)
Do not stop now... There's more after the ad ;)
What is hexagon?
Hexagon is any polygon that
has 6 sides, hence 6 vertices and 6 angles. As it is a polygon, it is a closed flat figure with sides that do not intersect. The hexagon is a recurring shape in nature, as in honeycombs, in structures of the organic chemistry, in the shells of certain turtles and in snowflakes.Video lesson about polygons
hexagon elements
A hexagon is made up of 6 sides, 6 vertices and 6 interior angles.
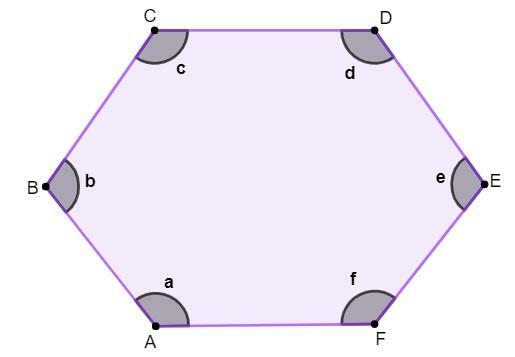
Vertices: points A, B, C, D, E, F.
sides: the segments \(\overline{AB},\overline{BC},\overline{CD},\overline{DE},\overline{EF},\ \overline{AF}\).
Internal angles: angles a, b, c, d, f.
Classification of hexagons
Hexagons, like other polygons, can be classified in two ways.
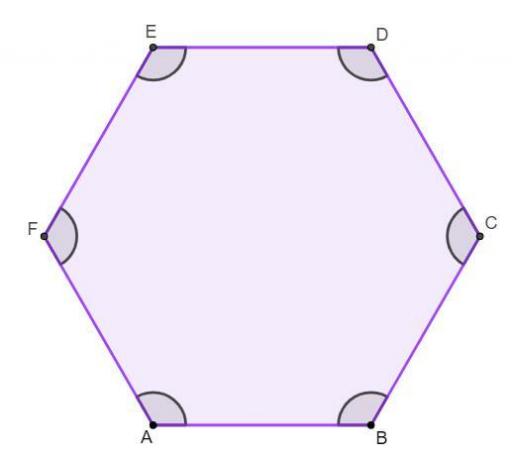
regular hexagon
The hexagon is regular when it has all its congruent sides — consequently, their angles will also be congruent. The regular hexagon is the most important of all, being the most widely studied. It is possible to calculate several of its aspects, such as the area, with specific formulas.
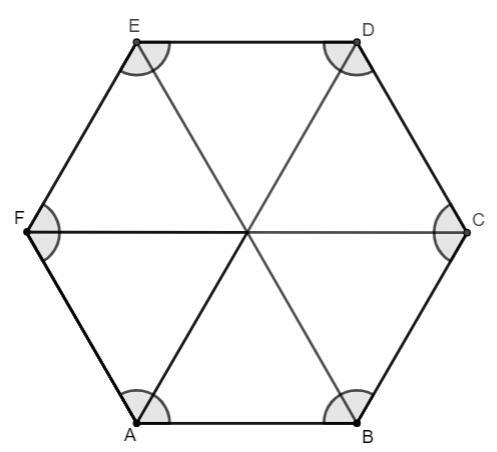
Observation: The regular hexagon can be divided into 6 equilateral triangles, that is, triangles with all sides equal.
→ irregular hexagon
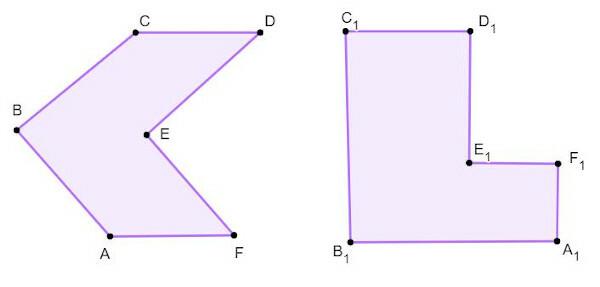
Irregular hexagon is one that has sides with different measures. It can be convex or non-convex.
convex irregular hexagon
the hexagon is convex when you have all the interior angles less than 180°.
→ Irregular non-convex hexagon
A hexagon is non-convex when it has interior angles greater than 180°.
hexagon properties
→ Number of diagonals in a hexagon
The first important property is that in a convex hexagon, there are always 9 diagonals. We can find these 9 diagonals geometrically:

We can also find the diagonals algebraically, using the following formula:
\(d=\frac{n\left (n-3\right)}{2}\)
If we substitute 6 into the equation, we have:
\(d=\frac{6\cdot\left (6-3\right)}{2}\)
\(d=\frac{6\cdot3}{2}\)
\(d=\frac{18}{2}\)
\(d=9\)
So a convex hexagon will always have 9 diagonals.
Know more: Rectangular block diagonal — segment connecting two of its vertices that are not on the same face
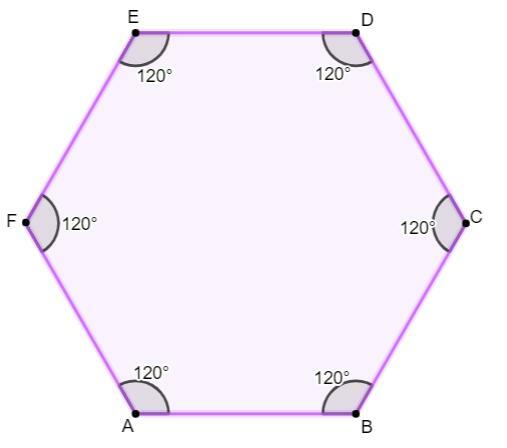
→ Interior angles of a hexagon
In a hexagon, the sum of its interior angles is 720°. To perform this sum, simply substitute 6 in the formula:
\(S_i=180\left (n-2\right)\)
\(S_i=180\left (6-2\right)\)
\(S_i=180\cdot4\)
\(S_i=720\)
In a regular hexagon, the interior angles will always measure 120° each, because
720°: 6 = 120°
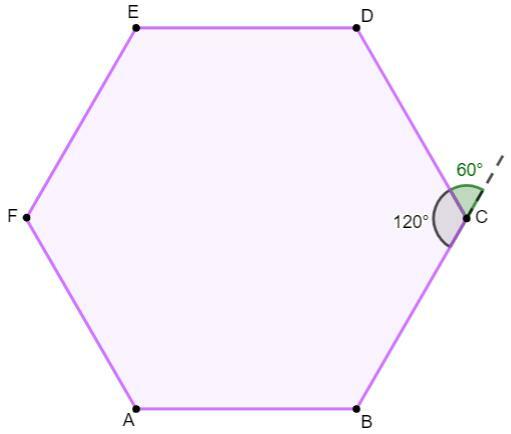
→ Exterior angles of a regular hexagon
As for the exterior angles, we know that the Their sum is always equal to 360°. Since there are 6 exterior angles, each of them will measure 60°, as
360°: 6 = 60°
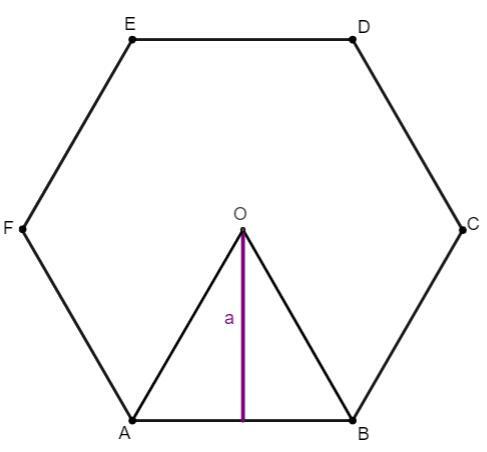
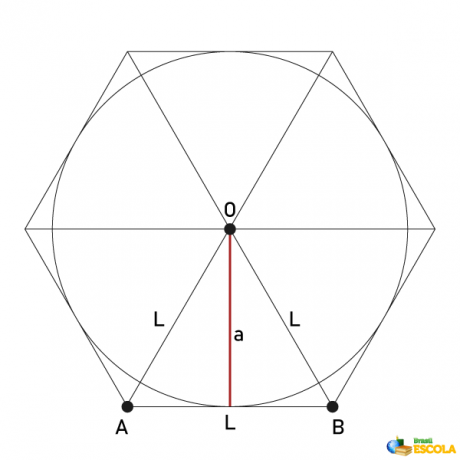
→ Regular hexagon apothem
An apothem of a regular polygon is considered to beline segment connecting the center of the polygon to the midpoint on your side. As we know, the regular hexagon is composed of 6 equilateral triangles, so the apothem corresponds to the height of one of these equilateral triangles. The value of this segment can be calculated by the formula:
\(a=\frac{L\sqrt3}{2}\)
→ perimeter of the hexagon
To calculate the perimeter of a hexagon, simply perform the sum of its 6 sides. When the hexagon is regular, its sides are congruent, so it is possible to calculate the perimeter of the hexagon using the formula:
P = 6L

→ regular hexagon area
As we know that the regular hexagon is composed of 6 equilateral triangles of sides measuring L, it is possible to derive a formula for the calculation of its area, using the calculation of the area of one triangle equilateral multiplied by 6.
\(A=6\cdot\frac{L^2\sqrt3}{4}\)
Note that it is possible to simplification dividing by 2, then generating the formula for calculating the area of the hexagon:
\(A=3\cdot\frac{L^2\sqrt3}{2}\)
Hexagon inscribed in a circle
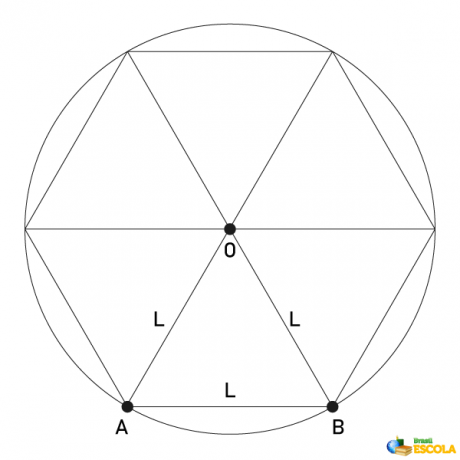
We say that a polygon is inscribed in a circumference when he is inside the circle, and its vertices are points of this. We can represent the regular hexagon inscribed in a circle. When we make this representation, it is possible to verify that the length of the radius of the circle is equal to the length of the side of the hexagon.
Also know: Circle and Circumference — What's the Difference?
Hexagon circumscribed in a circle
We say that a polygon is circumscribed by a circle when the circumference is inside this polygon. We can represent the circumscribed regular hexagon. In this case, the circle is tangent to the midpoint of each side of the hexagon, which makes the radius of the circle equal to the apothem of the hexagon.
hexagonal based prism
THE Plane Geometry is the basis for studies of Spatial Geometry. O hexagon may be present at the base of geometric solids, as in prisms.
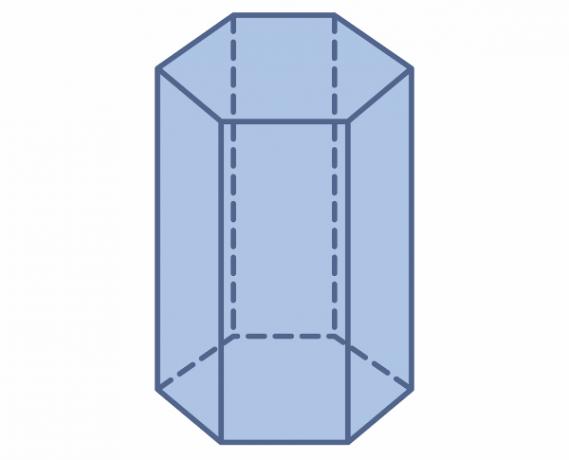
To find the volume of a prism, we calculate the product of the area of the base and the height. Since its base is a hexagon, its volume can be calculated by:
\(V=3\cdot\frac{L^2\sqrt3}{2}\cdot h\)
Read too: Volume of geometric solids — how to calculate?
Hexagonal base pyramid
In addition to the hexagonal prism, there are also the pyramids hexagonal base.
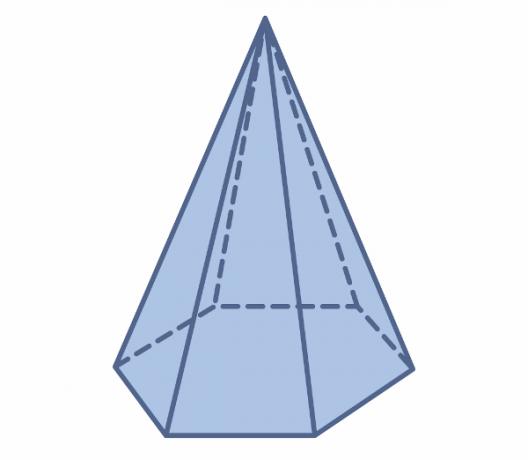
to discover the volume of a pyramid of hexagonal base, we calculate the product of the area of the base, the height and divide by 3.
\(V=3\cdot\frac{L^2\sqrt3}{2}\cdot h: 3\)
Note that we multiply and divide by three, which allows for a simplification. So, the volume of a hexagonal-based pyramid is calculated by the formula:
\(V=\frac{L^2\sqrt3}{2}\cdot h\)
Solved exercises on hexagon
question 1
A land is shaped like a regular hexagon. You want to surround this area with barbed wire, so that the wire goes around the territory 3 times. Knowing that, in all, 810 meters of wire were spent to fence the entire land, the area of this hexagon measures, approximately:
(Use \(\sqrt3=1.7\))
A) 5102 m²
B) 5164 m²
C) 5200 m²
D) 5225 m²
E) 6329 m²
Resolution:
Alternative B
The perimeter of the regular hexagon is
\(P=6L\)
As 3 laps were made, a total of 270 meters was spent to complete a single lap, as we know that:
810: 3 = 270
So we have:
\(6L=270\)
\(L=\frac{270}{6}\)
\(L=45\ meters\)
Knowing the length of the side, we will calculate the area:
\(A=3\cdot\frac{L^2\sqrt3}{2}\)
\(A=3\cdot\frac{{45}^2\sqrt3}{2}\)
\(A=3\cdot\frac{2025\sqrt3}{2}\)
\(A=3\cdot1012.5\sqrt3\)
\(A=3037.5\sqrt3\)
\(A=3037.5\cdot1.7\)
\(A=5163.75m^2\)
Rounding, we get:
\(A\approx5164m^2\)
question 2
(PUC - RS) For a mechanical gear, you want to make a part with a regular hexagonal shape. The distance between the parallel sides is 1 cm, as shown in the figure below. The side of this hexagon measures ______ cm.
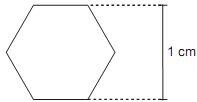
THE) \(\frac{1}{2}\)
B) \(\frac{\sqrt3}{3}\)
Ç) \(\sqrt3\)
D) \(\frac{\sqrt5}{5}\)
E) 1
Resolution:
Alternative B
Regarding the regular hexagon, we know that its apothem is the measure from the center to the midpoint of one of the sides. Thus, the apothem is half the distance indicated in the image. So, we have to:
\(2a=1cm\)
\(a=\frac{1}{2}\)
The apothem is then equal to \(\frac{1}{2}\). There is a relationship between the sides of the hexagon and the apothem, because in a regular hexagon, we have:
\(a=\frac{L\sqrt3}{2}\)
Since we know the value of the apothem, we can substitute \(a=\frac{1}{2}\) in the equation:
\(\frac{1}{2}=\frac{L\sqrt3}{2}\)
\(1=L\sqrt3\)
\(L\sqrt3=1\)
\(L=\frac{1}{\sqrt3}\)
Rationalizing the fraction:
\(L=\frac{1}{\sqrt3}\cdot\frac{\sqrt3}{\sqrt3}\)
\(L=\frac{\sqrt3}{3}\)
By Raul Rodrigues de Oliveira
Maths teacher


