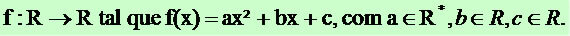A mathematical function can be classified as even or odd, depending on some characteristics. Also known as parity, it indicates whether they are symmetric about the y-axis or the origin of a Cartesian system.
Functions are expressions that take x values and transform them into y values, following the operations in their formation law. As this set of ordered pairs (x, y) are scored on a Cartesian plane, they form a graph.
Even functions produce graphs symmetric to the y-axis and odd functions symmetric to the origin of the Cartesian system.
A function without parity is that it has none of these characteristics, that is, it is neither even nor odd.
odd function
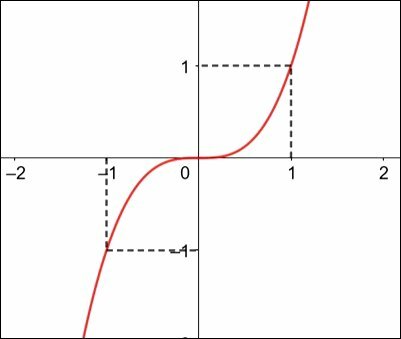
A function is odd when f(-x) = -f(x). This means that the values assumed by the function will be symmetrical both in relation to the x axis and in relation to the y axis.
Example
Function f: R→R defined by .
| x | f (x) | and |
|---|---|---|
| -1 | -1 | |
| 0 | 0 | |
| 1 | 1 |
We verify that f(-1) = -f(1) = -1, so the function is odd and its graph is symmetric about the origin.
even function
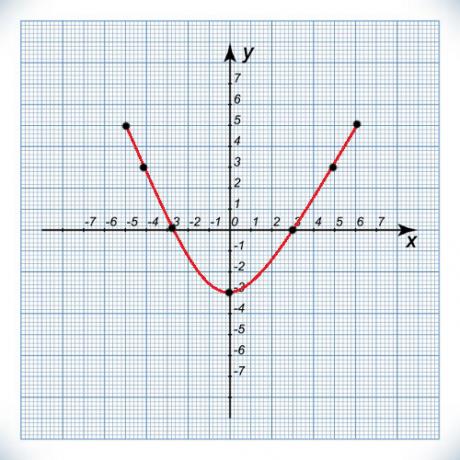
A function is even when f(-x) = f(x). This means that the value assumed by the function at points x and -x are equal. In this way, we can say that the function assumes equal values for symmetric x-values.
Example
Function f: R→R defined by .
| x | f (x) | and |
|---|---|---|
| -3 | 3 | |
| 0 | 0 | |
| 3 | 3 |
We verify that f(-3) = f(3) = 3, so that the function is even and its graph is symmetric about the y-axis.

learn more about functions.
Perhaps you are interested in:
- Domain, co-domain and image
- Surjective Function
- Bijection Function
- injection function
- Inverse Function
- Composite Function