Every function established by the formation law f (x) = ax² + bx + c, with a, b and c real numbers and a ≠ 0, is called a 2nd degree function. Generalizing we have:

2nd degree functions have many applications in everyday life, especially in physics-related situations involving uniformly varied motion, oblique throwing, etc.; in Biology, studying the photosynthesis process of plants; in Administration and Accounting relating the cost, revenue and profit functions; and in Civil Engineering present in the various constructions.
The geometric representation of a function of the 2nd degree is given by a parabola, which according to the sign of the coefficient The it may be concave up or down.
The roots of a 2nd degree function are the points where the parabola intersects the x-axis. Given the function f (x) = ax² + bx + c, if f (x) = 0, do we get a 2nd degree equation, ax² + bx + c = 0, depending on the value of the discriminant? (delta), we can have the following graphic situations:
? > 0, the equation has two real and different roots. The parabola intersects the x-axis at two distinct points.

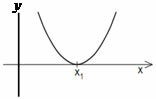
? = 0, the equation has only one real root. The parabola intersects the x-axis at a single point.
Do not stop now... There's more after the advertising ;)
? < 0, the equation has no real roots. The parabola does not intersect the x-axis.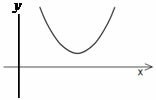
by Mark Noah
Graduated in Mathematics
See more!
2nd degree function signs
Concavity facing up and down.
2nd degree function graph
Representation of a 2nd degree function in the Cartesian plane.
Roots of a 2nd degree function
Root Sum and Product
Would you like to reference this text in a school or academic work? Look:
SILVA, Marcos Noé Pedro da. "Function of 2nd Degree"; Brazil School. Available in: https://brasilescola.uol.com.br/matematica/funcao-segundo-grau.htm. Accessed on June 28, 2021.