THE 2nd degree function or quadratic function is occupation real domain, ie any real number can be the x and, to each real number x, we associate a number of the form ax² + bx + c.
In other words, the quadratic function f is defined by:
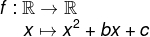
Next, we will see how to calculate this type of function, recalling Bhaskara's formula for finding the roots of the function, besides knowing the type of graph, its elements and how to draw it based on the interpretation of the data obtained by the solution.

What is a 2nd degree function?
A function f: R à → is called a 2nd degree function or quadratic function when there is a, b, c € R with a ≠ 0, so that f(x) = ax2 + bx + c, for all x € R.
Examples:
- f (x) = 6x2 - 4x + 5 → The = 6; B = -4; ç = 5.
- f(x) = x2 - 9 → The = 1; B = 0; ç = -9.
- f (x) = 3x2 +3x → The = 3; B = 3; ç = 0.
- f(x) = x2 – x → The = 1; B = -1; ç = 0.
for each real number x, we must replace and carry out the necessary operations to find your picture. See the following example:
Let's determine the image of the real number -2 of the function f(x) = 6x2 - 4x + 5. To do this, just replace the real number given in the function, like this:
f(-2) = 6(-2)2 – 4(-2) +5
f (-2) = 6(4) + 8 +5
f (-2) = 24 + 8 + 5
f(-2) = 37
Hence, the image of the number -2 is 27, resulting in the ordered pair (-2; 37).
Read too: 2nd degree equation: the equation that has an exponent 2 unknown
Do not stop now... There's more after the advertising ;)
Graph of the quadratic function
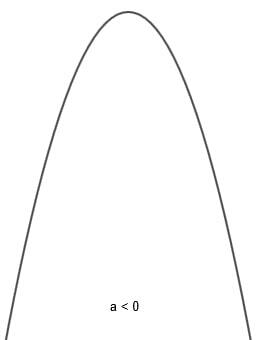
When sketching the quadratic function graph, we found a curve, which we'll call parable. Your concavity depends on the coefficientThe of the function f. When the function has the coefficient The greater than 0, the parabola will be concave upwards; when the coefficient The is less than 0, the parabola will be concave down.

Roots of the quadratic function
The roots of a quadratic function provide the points of intersection of the graph of the function with the axes of the Cartesian plane. When we consider a quadratic function of the form y = ax2 + bx + c and we initially take the x = 0, let's find the intersection with the O axisY. Now if we take the y = 0, let's find the intersection with axis OX,that is, the roots of the equation provide the intersection with the X axis. See an example:
a) y = x2 – 4x
Let's take x = 0 and substitute it into the given function. So, y = 02 – 4 (0) = 0. Note that when x = 0, we have y = 0. So we have the following ordered pair (0, 0). This ordered pair gives the y-intercept. Now, taking y = 0 and substituting into the function, we'll get the following:
x2 – 4x = 0
x.(x - 4) = 0
x’ = 0
x’’-4 = 0
x’’ = 4
Therefore, we have two points of intersection (0, 0) and (4, 0) and, in the Cartesian plane, we have the following:

Realize that we can use the relationship of bhaskara to find the zeros of the function. With this, we gain a very important tool: looking at the discriminant, we can know in how many places the graph intersects the X axis.
- If the delta is greater than zero (positive), the graph “cuts” the x axis into two points, that is, we have x’ and x’’.
- If the delta is equal to zero, the graph “cuts” the x-axis at a point, that is, x’ = x’’.
- If the delta is less than zero (negative), the graph does not “cut” the x-axis as there are no roots.
solved exercises
Question 1 - Given the function f (x) = -x2 + 2x – 4. Determine:
a) The intersection with the O axisY.
b) The intersection with the O axisX.
c) Sketch the graph of the function.
Solution:
a) To determine the intersection with the O axisY , just take the value of x =
b) 0. -(0)2 +2(0) – 4
0 + 0 – 4
-4
So we have the ordered pair (0, -4).
c) To find the intersection with the O axisX, just take the value of y = 0. Thus:
-x2 +2x – 4 = 0
Using Bhaskara's method, we have to:
Δ = b2 - 4ac
Δ = (2)2 - 4(-1)(-4)
Δ = 4 - 16
Δ = -12
Since the value of the discriminant is less than zero, the function does not intersect the X axis.
d) To sketch the graph, we must look at the points of intersection and analyze the concavity of the parabola. Since a < 0, the parabola will be concave downwards. Thus:

by Robson Luiz
Maths teacher
Calculate the value of k such that the function f(x) = 4x² – 4x – k has no roots, that is, the graph of the parabola has no point in common with the x-axis.
Determine the values of m so that the function f (x) = (m – 2)x² – 2x + 6 takes real roots.