Learn modular function with solved and annotated exercises. Clear your doubts with the resolutions and get ready for the entrance exams and competitions.
question 1
Which of the following represents the graph of the function f(x) = |x + 1| - 1, defined as .
The)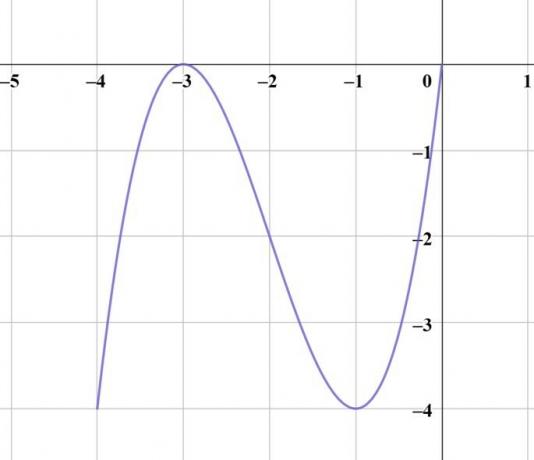
B)
ç)
d)
and)
Correct answer: e)
question 2
Write the formation law of the function f(x) = |x + 4| + 2, without module and in parts.
For
f (x) = x + 4 + 2 = x + 6
For
f (x) = - x - 4 + 2 = - x - 2
Therefore
question 3
Plot the graph of the function f(x) = |x - 5| - 1, defined as , in the range [0, 6].
The modular function |x - 5| -1, is formed, like the function |x|, by polygonal lines, that is, semi-straight lines with the same origin. The graph will be a horizontal translation to the right by five units and down by 1 unit.

question 4
The following graph represents the p(x) function. Plot the graph of the function q(x) such that q(x) = |p(x)|.
Below, the p(x) function is represented in red and the q(x) function in blue dashes.
The graph of q(x) is symmetrical to that of p(x) with respect to the x-axis.
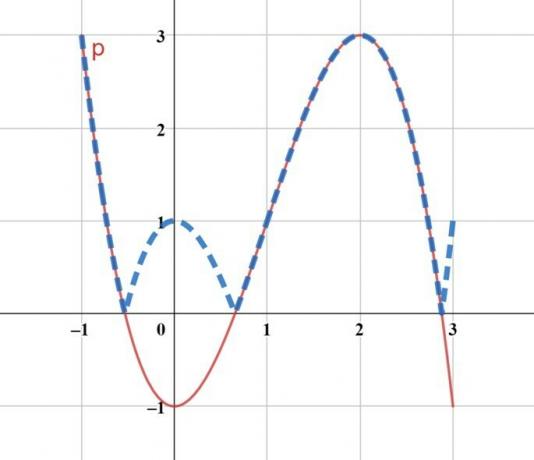
question 5
(Speck). Knowing that the graph below represents the real function f (x) = |x - 2| + |x + 3|, so the value of a + b + c is equal to

a) -7
b) -6
c) 4
d) 6
e) 10
Correct answer: c) 4.
Idea 1: Rewriting modules by parts.
We have two points of interest, x = 2 and x = -3. These points divide the number line into three parts.
Idea 2: identifying a and b.
Thus a = -3 and b = 2
In this case the order does not matter as we want to determine a + b + c, and in an addition the order does not change the sum.
Idea 3: Identifying the sentence of the modules for x greater than or equal to -3 and less than 2.
For
Idea 4: determining c.
Doing f(x) to
Thus, c = 5.
Therefore, the sum value: a + b + c = -3 + 2 + 5 = 4
question 6
EEAR (2016). Let f(x) = |x - 3| a function. The sum of the values of x for which the function takes the value 2 is
a) 3
b) 4
c) 6
d) 7
Correct answer: c) 6.
Idea 1: Values of x so that f (x) = 2.
We must determine the values of x for which f(x) takes the value 2.
Writing the function in parts and without the module notation we have:
In equation I, making f(x) = 2
2 = x - 3
2 + 3 = x
5 = x
In equation II, making f(x) = 2 and substituting
2 = - x + 3
2 - 3 = -x
-1 = -x
1 = x
Idea 2: adding the values of x that generated f (x) = 2.
5 + 1 = 6
Therefore, the sum of the values of x for which the function takes the value 2 is 6.
question 7
esPCEx(2008). Looking at the graph below, which represents the real function f (x) = |x - k| - p, it can be concluded that the values of k and p are, respectively,

a) 2 and 3
b) -3 and -1
c) -1 and 1
d) 1 and -2
e) -2 and 1
Correct answer: letter e) -2 and 1
Resolution
k translates the function horizontally and is the abscissa of its vertex.
For , the function is shifted to the right.
For , the function is shifted to the left.
So, since the function vertex has abscissa -2, this is the value of k.
p translates the function vertically.
For , the function is shifted up.
For , the function is shifted down.
Therefore, p = -1.
learn more about modular function.
You may be interested in:
Occupation
quadratic function
linear function
polynomial function
exponential function
Math Formulas



