Study with the 23 math exercises of the 7th year of Elementary with the themes studied in school. Clear all your doubts with the step-by-step template exercises.
The exercises are in accordance with the BNCC (Common National Curriculum Base). In each exercise you find the code of the skill worked. Use it in your classes and planning or as tutoring.
Exercise 1 (MDC - Maximum Common Divisor)
BNCC skill EF07MA01
Two-color blouses are being produced in one confection with the same amount of fabric for each color. In stock, there is a roll of white fabric measuring 4.2m and a roll of blue fabric measuring 13m. The fabrics must be cut into strips with the same and as long as possible, without any pieces left on the rolls. In centimeters, each strip of fabric will have
a) 150 cm.
b) 115 cm.
c) 20 cm.
d) 60 cm.
e) 32 cm.
Correct answer: c) 20 cm
To determine the length of the strips, which are the same and as large as possible, with no fabric left over on the rolls, we must determine the MDC between 420 cm and 1,300 cm.
Factoring between 420 and 1300.
Factoring both numbers at the same time, highlighting the divisors common to both and multiplying them:
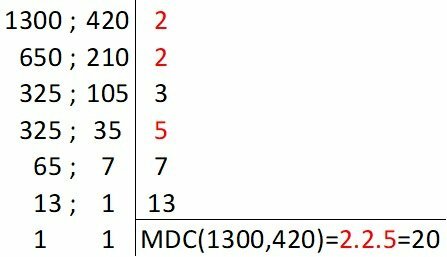
Therefore, the strips must have 20 cm so that there is no fabric on the rolls, having the largest possible size.
Exercise 2 (MMC - Minimum Common Multiple)
BNCC skill EF07MA01
Gabriel and Osvaldo are bus drivers on different lines. Early in the day, at 6 am, they agreed to have a coffee at the bus station the next time they meet. It turns out that Osvaldo's journey is longer and it takes him 2 hours to get back to the bus station, while Gabriel is at the bus station every 50 minutes. From 6 am, friends can have breakfast at
a) 6 am.
b) 8 am
c) 10 am
d) 12:00.
e) 16h.
Correct answer: e) 16h.
To determine when the two friends will meet again at the bus station, we must find the MMC - Minor Multiple Common between 2h, or 120 min and 50 min.
Factoring between 120 and 50.

Therefore, they will meet after 600 min or 10 h.
Starting at 6 am, they will meet at the bus station at 4 pm.
Exercise 3 (Parallel Lines Cut by a Transverse)
The line t is transversal to the parallels u and v. Check the option that determines the angle measurements and
, in this order.
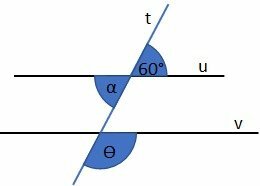
BNCC skill EF07MA23
a) 180° and 60°.
b) 60° and 90°.
c) 90° and 180°.
d) 120° and 60°.
e) 30° and 150°.
Correct answer: d) 120° and 60°.
the angle it is opposite at the apex to that of 60°, so it also has 60°.
the angle it is external collateral with the angle of 60°. These angles are supplementary, that is, added together they result in 180°. That is why,
= 120, because
Exercise 4 (Measurement of Length)
BNCC skill EF07MA29
This last Sunday, Caio went out riding his bike and decided to go to his friend José's house, covering 1.5 km. From there, the two cycled to Sabrina's house, which was on the next block, three hours later. The three friends decided to go to the top of the city's mountains, cycling another 4 km. From home, to the top of the mountain, how many meters did Caio pedal?
a) 5 500 m
b) 5800 m
c) 5 303 m
d) 5 530 m
e) 8 500 m
Correct answer: b) 5800 m
First we transform the measurements to meters.
1.5 km = 1500 m
3 hm = 300 m
4 km = 4 000 m
Exercise 5 (Measurement of Time)
BNCC skill EF07MA29
Maria will drop her son off at the cinema watching the new Radical Superheroes movie while shopping for a few things at the mall. She already knows that the film has 2h 17min, enough time to make the purchases. Turning in seconds, the movie has
a) 8 220 s.
b) 8 100 s.
c) 7 200 s.
d) 7 350 s.
e) 4 620 s.
Correct answer: a) 8 220 s.
First we transform in minutes.
2h 17min = 60 min + 60 min + 17 min = 137 min
Each minute is 60 seconds long. We multiply by 60.
137 min x 60 s = 8 220 s
Exercise 6 (Mass Measurement)
BNCC skill EF07MA29
In a 900 km journey, a car's on-board computer exhibited an emission of 117 kg of carbon dioxide. Some time later, this equipment was damaged and it was not calculating this information. Based on the data obtained from his trip, the car owner calculated the amount of CO2 emitted in a 25 km ride, finding in grams the amount of
a) 3250 g.
b) 192 307 g.
c) 325 g.
d) 192 g.
e) 32.5 g.
Correct answer: a) 3 250 g
1st step: amount of CO2 emitted per kilometer traveled.
2nd step: amount of CO2 emitted in 25 km.
3rd step: transforming from kg to g.
To transform from kg to g, we multiply by 1000.
3.25 kg = 3 250 g
Therefore, the amount in grams of CO2 emitted by the vehicle on a 25 km ride is 3 250 g.
Exercise 7 (Volume)
BNCC skill EF07MA30
A contractor is constructing a building and has closed a purchase of crushed stone, the material needed to make concrete. The gravel is delivered in trucks, with buckets in the form of cobblestones measuring 3 m x 1.5 m x 1 m. The engineers calculated a total volume of 261 m³ of gravel to carry out the work. The number of trucks that the contractor had to hire was
a) 81.
b) 64.
c) 36.
d) 48.
e) 58.
Correct answer: e) 58.
The volume of a parallelepiped is calculated by multiplying the measurements of the three dimensions.
The bucket volume of a truck is:
V = length x width x height
V = 3 x 1.5 x 1 = 4.5 m³
Dividing the total volume calculated for the work, 261 m³ by the volume of a bucket
The company should hire 58 gravel trucks.
Exercise 8 (Capacity)
BNCC skill EF07MA29
In long-distance running, it is common to distribute water to athletes. Support staff provide bottles or glasses of water at the edge of the track so runners can hydrate without stopping running. In a marathon, organizers distributed 3,755 glasses with 275 ml of water in each. The amount of water, in liters, consumed during the race was approximately
a) 1 l
b) 103.26 l
c) 1,033 l
d) 10.32 l
e) 10 326 l
Correct answer: c) 1 033 l
The total amount in milliliters was .
To transform the measure from milliliters to liters, we divide by 1000.
Approximately 1033 l.
Exercise 9 (Rectangle and Parallelogram Area)
BNCC skill EF07MA31
The city hall has land in the form of a parallelogram. It was decided that a multi-sport court will be built at the site, with stands on the sides. The remaining spaces will be decorated with gardens. According to the project's floor plan, each garden will occupy an area of
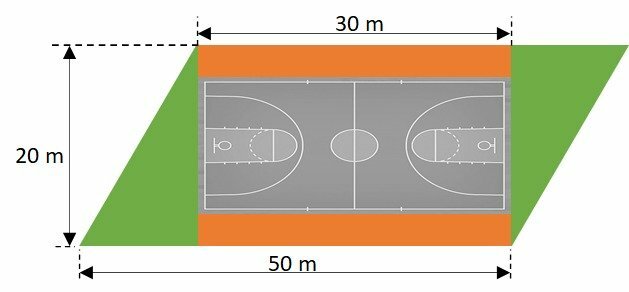
a) 200 m².
b) 250 m².
c) 300 m².
d) 350 m².
e) 400 m².
Correct answer: a) 200 m².
1st step: parallelogram area.
2nd step: rectangle area and bleachers.
3rd step: garden area, in green.
Subtracting the total area from the rectangle area.
Therefore, as the triangles are the same, the area of each garden is 200 m².
Exercise 10 (Diamond Area)
BNCC skill EF07MA31
Mr. Pompey likes to make kites. On the weekend there will be a kite fair and he will take some. How many square centimeters of tissue paper does he use to make a kite, depending on the model? Mark the correct option.
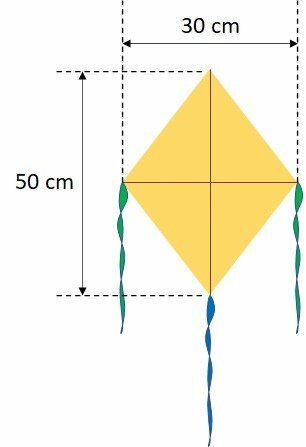
a) 7.5 m²
b) 0.075 m².
c) 0.15 m².
d) 0.75 m²
e) 1.5 m²
Correct answer: b) 0.075 m².
The kite is shaped like a diamond. The diagonal measurements are shown in the figure, in centimeters.
The area of a diamond is calculated by:
Therefore, in square meters, the kite area is 0.075 m².
Exercise 11 (Triangle and Hexagon Area)
BNCC skill EF07MA32
A regular hexagon is formed by six equilateral triangles with sides measuring 12 cm. The area of the hexagon is equal to
The) .
B) .
ç) .
d) .
and) .
Correct answer: b) .
We must calculate the area of a right triangle and multiply it by six.
1st step: determine the height of the triangle.
To calculate the height, we use the Pythagorean Theorem.
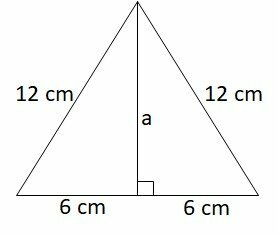
So the height of the triangle measures cm.
2nd step: calculate the area of an equilateral triangle.
Area is calculated by the product of base and height, divided by two.
3rd step: calculate the area of the hexagon.
Multiplying the area of the triangle by six, we have:
The square root of 108 has no exact solution, but it is common to factor the radical.

Therefore, the area of the hexagon is .
Exercise 12 (Length of Circumference)
BNCC skill EF07MA33
Bicycles have a number that identifies the size of their wheels. A 20-rim bicycle has wheels that are 20 inches in diameter, while a 26-rim bicycle has wheels that are 26 inches in diameter. What is the difference between the lengths of the wheel circumferences of a bicycle rim 26 and 20, in centimeters.
Given: 1 inch = 2.54 cm and = 3,14.
a) 47.85 cm
b) 18.84 cm
c) 29.64 cm
d) 34.55 cm
e) 55.17 cm
Correct answer: a) 47.85 cm
The length of the circle is calculated by the relation
The radius of the 26 rim bike is 13 inches.
The radius of the 20 rim bike is 10 inches.
1st step: calculation of the circumference of the bicycle rim 26.
2nd step: calculation of the circumference of the bicycle rim 20.
3rd step: difference between the circles
4th step: changing to centimeters
Exercise 13 (Condition of Existence of Triangles)
BNCC skill EF07MA25
Of the following trios of measurements below, it is possible to assemble a triangle with just
a) 7, 3, 14.
b) 19, 3, 6.
c) 8, 15, 45.
d) 12, 15, 17.
e) 21, 13, 7.
Correct answer: d) 12, 15, 17.
To determine whether a triangle can be constructed from three measurements, we run three tests. The measurement of each side must be less than the sum of the other two sides.
Test 1: 12 < 15 + 17
Test 2: 15 < 12 + 17
Test 3: 17 < 15 + 12
As the inequalities of the three tests are true, a triangle with these measures exists.
Exercise 14 (Sum of the Angles of Triangles)
BNCC skill EF07MA24
In the triangle in the figure, determine the value of the angles of the vertices A, B and C and check the correct option.
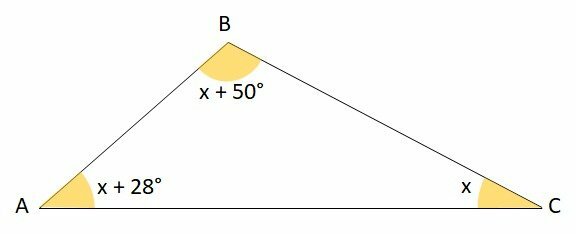
a) A = 64°, B = 34° and C = 82°
b) A = 62°, B = 84° and C = 34°
c) A = 53°, B = 62° and C = 65°
d) A = 34°, B = 72° and C = 74°
e) A = 34°, B = 62° and C = 84°
Correct answer: b) A = 62°, B = 84° and C = 34°.
The sum of all the interior angles of a triangle always results in 180°.
Soon,
A = x + 28 = 34 + 28 = 62°
B = x + 50 = 34 + 50 = 84°
C = x = 34°
Exercise 15 (Equation of the 1st degree)
BNCC skill EF07MA18
Using 1st degree equations with one unknown, express each situation below and determine its root.
a) A number subtracted from its third plus its double equals 26.
b) The quadruple of a number added to the number itself and subtracted from a fifth of the number is equal to 72.
c) The third of a number added to its quintuplet is equal to 112.
The)
B)
ç)
Exercise 16 (Equation of the 1st degree)
BNCC Skill EF07MA18 and EF07MA16
Three consecutive numbers added together make 57. Determine what the numbers in this sequence are.
a) 21, 22 and 23
b) 10, 11 and 12
c) 27, 28 and 29
d) 18, 19 and 20
e) 32, 33 and 34
Correct answer: d) 18, 19 and 20
Calling x the middle number of the sequence, we have:
Substituting 19 by x in the first line, we find:
(19 - 1) + 19 + (19 + 1) = 57
Thus, the numbers are:
18, 19 and 20
Exercise 17 (Reason)
BNCC skill EF07MA09
Mariana's class at the school has 23 students, 11 of whom are boys. The ratio between the number of boys and girls in Mariana's class is
a) 11/23
b) 12/23
c) 11/12
d) 12/11
e) 12/12
Correct answer: d) 12/11
Reason is a relationship described through a fraction.
As in Mariana's classroom there are 23 students and 11 are boys, the number of girls is:
23 -11=12
So there are 11 boys for every 12 girls. The ratio between the number of boys and girls in Mariana's classroom is:
Exercise 18 (Reason)
BNCC skill EF07MA09
According to IBGE data, Brazil's population statistics in 2021 is 213.3 million inhabitants. The approximate area of the Brazilian territory is 8,516,000 km². Based on these data, the Brazilian demographic density is of
a) 15 people.
b) 20 people.
c) 35 people.
d) 40 people.
e) 45 people.
Correct answer: 25 people.
Demographic density is the number of people who live in an area. We want to determine, according to IBGE population statistics for the year 2021, how many people live per square kilometer in Brazil.
In the form of reason, we have:
Therefore, the population density in the year 2021 is approximately 25 people per square kilometer.
Exercise 19 (Proportion - Directly proportional quantities)
BNCC skill EF07MA17
If a vehicle has an autonomy of 12 km with a liter of fuel, with 23 liters, this vehicle can travel, without stopping to refuel
a) 113 km.
b) 156 km.
c) 276 km
d) 412 km.
e) 120 km.
Correct answer: c) 276 km.
The proportionality is direct between the quantities of liters of fuel and kilometers traveled because, the more fuel, the greater distance the vehicle can move.
We set up the ratio between the ratios:
A liter is for 12 km, just as 23 liters is for x.
Using the fundamental property of proportions (cross multiplication), we determine the value of x.
Thus, with 23 liters of fuel, the vehicle will be able to travel 276 km.
Exercise 20 (Percentage)
BNCC skill EF07MA02
The fuel used in motor vehicles is actually a mixture, even when the consumer buys gasoline at a gas station. This is because Law 10,203/01 established that gasoline must contain between 20% and 24% of fuel alcohol. Afterwards, the National Petroleum Agency (ANP) set the alcohol-gasoline mixture at 23%.
If a customer at a gas station asks the attendant to fill the tank with gasoline and the pump reads 50 liters, of these, the real amount of pure gasoline is
a) 11.5 l.
b) 38.5 l.
c) 45.5 l.
d) 35.5l.
e) 21.5 l.
Correct answer: b) 38.5 l.
According to the ANP, the percentage of alcohol mixed in gasoline is 23%.
Every 50 liters, 11.5 l is alcohol.
Thus, of the 50 liters of fuel supplied, the amount of pure gasoline is
Exercise 21 (Proportion - Inversely Proportional Quantities)
BNCC skill EF07MA17
A train travels 90 km in 1.5 h at a constant speed of 60 km/h. Suppose a person has traveled the same distance by car at a speed of 100 km/h. The time of this trip in hours will be
a) 30 min.
b) 43 min.
c) 54 min.
d) 61 min.
e) 63 min.
Correct answer: c) 54 min.
The quantity time is inverse to speed because, the higher the speed, the shorter the travel time.
We set up the ratio between the ratios:
60 km/h is for 1.5 hours of travel, just as 100 km/h is for x.
Attention, as the magnitudes are inverse, we must invert the reason where the unknown is.
Applying the fundamental property of proportions, we make the product of means equal to the product of extremes.
Thus, the person who traveled the same path at a speed of 100 km/h took 0.9 h to complete the path.
turning in minutes
0.9 x 60 = 54
In minutes, the person who traveled by car took 54 minutes to complete the journey.
Exercise 22 (Rule of Three Compound)
BNCC skill EF07MA17
In a production, six seamstresses produce 1200 pieces in three days of work. The number of pieces produced by eight seamstresses in nine days will be
a) 4800 pieces.
b) 1600 pieces.
c) 3600 pieces.
d) 2800 pieces.
e) 5800 pieces.
Correct answer: a) 4800 pieces.
The number of pieces is directly proportional to the number of seamstresses and working days.
| number of seamstresses | number of working days | number of pieces |
|---|---|---|
| 6 | 3 | 1 200 |
| 8 | 9 | x |
We have two ways to solve it.
1st way
The ratio of the unknown x, is equal to the product of the other ratios.
2nd way
We make the equality between the reason of the unknown and any other, setting a magnitude.
Fixing in three days.
In three days, six seamstresses produce 1 200 pieces, as well as 8 seamstresses produce x.
We now know that eight seamstresses produce 1600 pieces in three days, but we want to know how many pieces the 8 seamstresses produce in nine days. Now, we use the other reason.
Eight seamstresses produce 1600 pieces in three days, as well as produce x pieces in nine days.
Therefore, eight seamstresses working nine days produce 4,800 pieces.
Exercise 23 (Probability)
BNCC skill EF07MA36
A survey carried out with residents of two cities in relation to the brands of two cafes, interviewed residents in relation to their preferences. The result is shown in the table:
| coffee sweet flavor | Spice Coffee | |
|---|---|---|
| Residents of city A | 75 | 25 |
Residents of city B |
55 | 65 |
BNCC skill EF07MA34 and EF07MA36
The Especiaria Café brand will give away a kit of products for one of the interviewees. The probability of the winner having this brand as a preference and still being a resident of city A is
a) 16.21%
b) 15.32%
c) 6.1%
d) 25.13%
e) 11.36%
Correct answer: e) 11.36%
Whether the random experiment draws a random respondent, event C is the one drawn from city A and prefers Especiaria Café.
The number of elements in the sample space is:
75 + 25 + 55 + 65 = 220
The probability of event C occurring is calculated by:
To determine the percentage, we divide the numerator by the denominator and multiply the result by 100.
Therefore, the probability of the winner having Especiaria Café as a preference and still being a resident of city A is 11.36%.
See too
- Mathematics exercises 6th year
- Exercises on measures of length
- Exercises on parallel lines cut by a transversal
- Exercises on simple rule of three
- Exercises on 1st degree equation with an unknown
- Probability exercises solved (easy)
- Exercises in reason and proportion
- Rule of Three Compound Exercises
- MMC and MDC - Exercises
- Flat Figures Area - Exercises
- Percentage Exercises
- Probability Exercises


