Exercises on potential and kinetic energy

Study about kinetic and potential energy with this list of solved exercises that Toda Matter has prepared for you. He solves his doubts with step-by-step resolutions and prepares himself with ENEM and entrance exam questions.

question 1

In a market, two workers are loading a truck that will deliver vegetables. The operation takes place as follows: worker 1 removes the vegetables from a stall and keeps them in a wooden box. Afterwards, he throws the box, making it slide on the ground, towards worker 2 who is beside the truck, in charge of storing it on the body.

Worker 1 throws the box with an initial speed of 2 m/s and the friction force performs a modulus job equal to -12 J. The wooden box plus vegetables set has a mass of 8 kg.
Under these conditions, it is correct to state that the speed at which the box reaches worker 2 is

a) 0.5 m/s.
b) 1 m/s.
c) 1.5 m/s.
d) 2 m/s.
e) 2.5 m/s.

See Answer

Correct answer: b) 1 m/s

The work of the forces acting on a body is equal to the change in the energy of that body. In this case, kinetic energy.

The change in kinetic energy is the final kinetic energy minus the initial kinetic energy.

From the statement, we have that the work is - 16 J.

The speed at which the box reaches worker 2 is the final speed.

Solving for Vf

Therefore, the speed at which the box reaches worker 2 is 1 m/s.

question 2

In a bagged grain warehouse, a large shelf with four shelves 1.5 m high stores the goods that will be shipped. Still on the ground, six sacks of grain weighing 20 kg each are placed on a wooden pallet, which is collected by a forklift. Each pallet has 5 kg of mass.

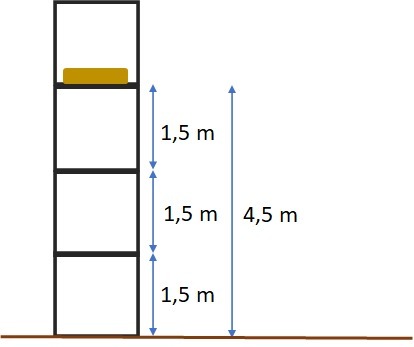
Considering the acceleration of gravity equal to 10 m/s², the set bags plus pallet as a body and disregarding its dimensions, the energy gravitational potential acquired by the pallet set plus bags of grain, as they leave the ground and are stored on the fourth floor of the shelf, stands for

a) 5400 J.
b) 4300 J.
c) 5 625 J.
d) 7200 J.
e) 7,500 J.

See Answer

Correct answer: c) 5 625 J

The gravitational potential energy of a body is the product of the mass of that body, the magnitude of the acceleration due to gravity and its height in relation to the ground.

Calculation of mass

As each bag of grain has 20 kg of mass and the pallet is 5 kg, the set has:

20.6 + 5 = 120 + 5 = 125 kg

The height

The bookcase has 4 floors of 1.5 m and the set will be stored on the fourth. Its height will be 4.5 m from the ground, as shown in the drawing. Note that the set is not on the fourth floor but on the fourth floor.

Thus:

The energy acquired by the set will be 5 625 J.

question 3

A spring that has a length of 8 cm when at rest receives a compressive load. An 80 g mass body is placed over the spring and its length is reduced to 5 cm. Considering the acceleration of gravity as 10 m/s² determine:

a) The force acting on the spring.
b) The elastic constant of the spring.
c) The potential energy stored by the spring.

See Answer

a) The force acting on the spring corresponds to the weight force exerted by the 80 g mass.

The force weight is obtained by the product of mass and the acceleration due to gravity. It is necessary that the mass is written in kilograms.

80 g = 0.080 kg.

The force acting on the spring is 0.80 N.

b) In the vertical direction, only the weight force and the elastic force act, in opposite directions. Once static, the elastic force cancels out with the weight force, having the same modulus.

The deformation x was 8 cm - 5 cm = 3 cm.

The relationship that provides the tensile strength is

where k is the elastic constant of the spring.

c) The potential energy stored in a spring is given by the equation of work of elastic force.

Replacing the values ​​in the formula and calculating, we have:

in scientific notation

question 4

A body with a mass equal to 3 kg is free-falling from a height of 60 m. Determine the mechanical, kinetic and potential energy at times t = 0 and t = 1s. Consider g = 10 m/s².

See Answer

Mechanical energy is the sum of kinetic and potential energy at each instant.

Let's calculate the energies for t = 0s.

Kinetic energy at t = 0s.

At t=0s the speed of the body is also zero, as the body is abandoned, leaving rest, so the kinetic energy is equal to 0 Joules.

Potential energy at t = 0s.

Mechanical energy at t = 0s.

Let's calculate the energies for t = 1s.

Kinetic energy at t = 1s.

First, it is necessary to know the velocity at t=1s.

For this, we will use the hourly velocity function for a MUV (uniformly varied movement).

Where,
is the initial speed,
The is the acceleration, which in this case will be the acceleration of gravity, g,
t is the time in seconds.

The initial movement speed is 0, as we've already seen. The equation looks like this:

Using g = 10 and t = 1,

Which means that in 1s of fall the velocity is 10 m/s and now we can calculate the kinetic energy.

Potential energy for t=1s.

To know the potential energy at t=1s, we first need to know how high it is at this instant. In other words, how far it has shifted. For that, we will use the hourly function of the positions for t=1s.

Where, is the starting position of the move, which we will consider as 0.

Therefore, at t=1s the body will have traveled 5 m and its height in relation to the ground will be:

60 m - 5 m = 55 m

Now we can calculate the potential energy for t=1s.

Calculating mechanical energy for t=1s.

See that the mechanical energy is the same, I try for t = 0s as for t = 1s. As the potential energy decreased, the kinetics increased, compensating for the loss, as it is a conservative system.

question 5

A child is playing on a swing in a park with his father. At a certain point, the father pulls the swing, raising it to a height of 1.5 m in relation to where it is at rest. The swing set plus child has a mass equal to 35 kg. Determine the horizontal speed of the swing as it passes through the lowest part of the trajectory.

Consider a conservative system where there is no energy loss and the acceleration due to gravity is equal to 10 m/s².

See Answer

All potential energy will transform into kinetic energy. In the first moment the potential energy is

In the second instant the kinetic energy will be equal to 525 J because all potential energy becomes kinetic.

Therefore, the horizontal velocity of the body is , or approximately 5.47 m/s.

question 6

(Enem 2019) At a science fair, a student will use the Maxwell disk (yo-yo) to demonstrate the principle of energy conservation. The presentation will consist of two steps:

Step 1 - the explanation that, as the disk descends, part of its gravitational potential energy is transformed into kinetic energy of translation and kinetic energy of rotation;

Step 2 - the calculation of the kinetic energy of rotation of the disk at the lowest point of its trajectory, assuming the conservative system.

When preparing the second step, he considers the acceleration due to gravity equal to 10 m/s² and the linear velocity of the center of mass of the disk negligible compared to the angular velocity. It then measures the height of the top of the disc relative to the ground at the lowest point of its trajectory, taking 1/3 of the height of the toy's shank.

The toy's size specifications, that is, of length (L), width (L) and height (H), as well as from the mass of its metal disk, were found by the student in the clipping of the illustrated manual to follow.

Contents: metal base, metal rods, top bar, metal disc.
Size (L × W × H): 300mm × 100mm × 410mm
Metal disk mass: 30 g

The result of the calculation of step 2, in joule, is:

See Answer

Correct answer: b)

We want to determine the kinetic energy of rotation at time 2, when the disk is at its lowest position.

Since the translation energy has been neglected, and there are no energy losses, all gravitational potential energy is transformed into kinetic energy of rotation.

Kinetic energy of rotation at the lowest point of the trajectory = Potential gravitational energy at the highest point of the trajectory.

The total height of the set is 410 mm or 0.41 m. The height of the trajectory is it's the same as:

The mass is 30 g, in kilograms, 0.03 kg.

Calculating potential energy.

In scientific notation, we have

question 7

(CBM-SC 2018) Kinetic energy is energy due to motion. Everything that moves has kinetic energy. Therefore, moving bodies have energy and therefore can cause deformations. The kinetic energy of a body depends on its mass and speed. Therefore, we can say that kinetic energy is a function of the mass and velocity of a body, where kinetic energy is equal to half its mass times its velocity squared. If we do some calculations, we will find that velocity determines a much greater increase in kinetic energy than mass, so we can conclude that there will be much greater injuries to occupants of a vehicle involved in a high-speed crash than to those in a low-speed crash velocity.

It is known that two cars, both weighing 1500 kg, collide in the same barrier. Car A has a speed of 20 m/s and vehicle B a speed of 35 m/s. Which vehicle will be more susceptible to a more violent collision and why?

a) Vehicle A, as it has a higher speed than vehicle B.
b) Vehicle B, as it has a constant speed higher than that of vehicle A.
c) Vehicle A, as it has the same mass as vehicle B, however it has a constant speed higher than vehicle B.
d) Both vehicles will be impacted with the same intensities.

See Answer

Correct answer: b) Vehicle B, as it has a constant speed higher than vehicle A.

As the statement says, kinetic energy increases with the square of velocity, so a higher velocity produces greater kinetic energy.

By way of comparison, even if it is not necessary to answer the problem, let's calculate the energies of two cars and compare them.

car A

car B

Thus, we see that the increase in the speed of car B leads to a kinetic energy more than three times greater than that of car A.

question 8

(Enem 2005) Observe the situation described in the strip below.

As soon as the boy shoots the arrow, there is a transformation from one type of energy to another. The transformation, in this case, is of energy

a) elastic potential in gravitational energy.
b) gravitational into potential energy.
c) elastic potential in kinetic energy.
d) kinetics in elastic potential energy.
e) gravitational into kinetic energy

See Answer

Correct answer: c) elastic potential in kinetic energy.

1 - The archer stores energy in the elastic potential form, by deforming the bow that will act as a spring.

2 - When releasing the arrow, the potential energy is transformed into kinetic energy, when it goes into motion.

question 9

(Enem 2012) A car, in uniform motion, walks along a flat road, when it starts to descend a slope, on which the driver makes the car always keep up with climbing speed constant.

During the descent, what happens to the potential, kinetic, and mechanical energies of the car?

a) The mechanical energy remains constant, since the scalar velocity does not vary and, therefore, the kinetic energy is constant.
b) The kinetic energy increases, as the gravitational potential energy decreases and when one decreases, the other increases.
c) The gravitational potential energy remains constant, as there are only conservative forces acting on the car.
d) Mechanical energy decreases, as kinetic energy remains constant, but gravitational potential energy decreases.
e) The kinetic energy remains constant as there is no work done on the car.

See Answer

Correct answer: d) Mechanical energy decreases as kinetic energy remains constant but gravitational potential energy decreases.

Kinetic energy depends on mass and velocity, as they do not change, kinetic energy remains constant.

The potential energy decreases as it depends on the height.

Mechanical energy decreases as this is the sum of potential energy plus kinetic energy.

question 10

(FUVEST 2016) Helena, whose mass is 50 kg, practices extreme sport bungee jumping. In a workout, it comes loose from the edge of a viaduct, with zero initial velocity, attached to an elastic band of natural length and elastic constant k = 250 N/m. When the swath is stretched 10 m beyond its natural length, Helena's modulus of velocity is

Note and adopt: gravity acceleration: 10 m/s². The band is perfectly elastic; its mass and dissipative effects should be ignored.

a) 0 m/s
b) 5 m/s
c) 10 m/s
d) 15 m/s
e) 20 m/s

See Answer

Correct answer: a) 0 m/s.

By energy conservation, the mechanical energy at the start of the jump is equal at the end of the jump.

at the beginning of the movement

The kinetic energy is 0 since the initial velocity is 0.
The elastic potential energy is 0 because the elastic band is not tensioned.

at the end of the movement

The gravitational potential energy is 0, relative to the length calculated at the beginning.

The balance of energies now looks like this:

Since we want speed, let's isolate kinetic energy from one side of equality.

doing the calculations

gravitational potential energy

h = 15 m of natural length of the strip + 10 m of stretch = 25 m.

elastic potential energy

Replacing the values ​​in the energy balance, we have:

As the kinetic energy only depends on the mass, which has not changed, and on the velocity, we have velocity equal to 0.

Identifying with calculation.

Equating the kinetic energy to 0, we have:

Therefore, when the strip is stretched 10 m beyond its natural length, Helena's modulus of velocity is 0 m/s.

question 11

(USP 2018) Two bodies of equal masses are released, at the same time, from rest, from height h1 and travel along the different paths (A) and (B), shown in the figure, where x1 > x2 and h1 > h2.

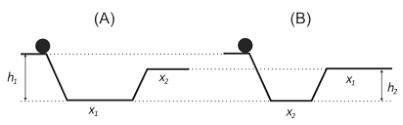
Consider the following statements:

I. The final kinetic energies of the bodies in (A) and (B) are different.
II. The mechanical energies of the bodies, just before they start to climb the ramp, are equal.
III. The time to complete the course is independent of the trajectory.
IV. The body in (B) reaches the end of the trajectory first.
V. The work performed by the weight force is the same in both cases.

It is correct only what is stated in

Note and Adopt: Disregard dissipative forces.

a) I and III.
b) II and V.
c) IV and V.
d) II and III.
e) I and V.

See Answer

Correct answer: b) II and V.

I - WRONG: As the initial energies are equal and dissipative forces are not considered and bodies A and B go down h1 and go up h2, only the potential energy changes, equally, for both.

II - CERTA: As dissipative forces are neglected, such as friction when traveling the paths until the beginning of the climb, the mechanical energies are equal.

III - WRONG: As x1 > x2, body A travels the trajectory of the "valley", the lower part, with greater speed for a longer time. As B starts to climb first, it already loses kinetic energy, decreasing its speed. Still, after the climb, both have the same speed, but body B needs to travel a greater distance, taking longer to complete the course.

IV - WRONG: As we saw in III, body B arrives after A, as it takes longer to complete the route.

V - RIGHT: As the weight force only depends on the mass, gravity acceleration and height difference during the journey, and they are equal for both, the work performed by the weight force is the same for both.

you keep practicing with kinetic energy exercises.

you may be interested in

• Potential energy
• Gravitational Potential Energy
• Elastic Potential Energy