Rule of Three Exercises

THE rule of three is a procedure used for solving problems involving quantities that are proportional.

Because it has a huge applicability, it is very important to know how to solve problems using this tool.

So, take advantage of the annotated exercises and resolved contest questions to check your knowledge of this subject.

Commented Exercises

Exercise 1

To feed your dog, a person spends 10 kg of feed every 15 days. What is the total amount of feed consumed per week, considering that the same amount of feed is always added per day?

Solution

We must always start by identifying the magnitudes and their relationships. It is very important to correctly identify whether the quantities are directly or inversely proportional.

In this exercise, the total amount of feed consumed and the number of days are directly proportional, as the more days, the greater the total amount spent.

To better visualize the relationship between the quantities, we can use arrows. The direction of the arrow points to the highest value of each magnitude.

The quantities whose pairs of arrows point in the same direction are directly proportional and those that point in opposite directions are inversely proportional.

Let's then solve the proposed exercise, as shown in the diagram below:

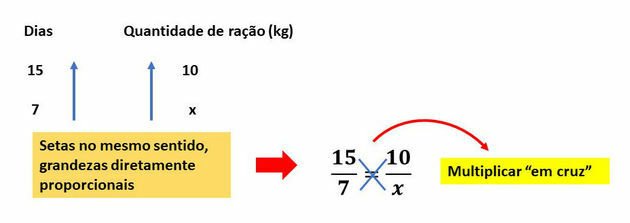
Solving the equation, we have:

Thus, the amount of feed consumed per week is approximately 4.7 kg.

See too: Ratio and Proportion

Exercise 2

A tap fills a tank in 6 h. How long will the same tank take to fill if 4 taps with the same flow rate as the previous tap are used?

Solution

In this problem, the quantities involved will be number of taps and time. However, it is important to note that the greater the number of taps, the less time it takes to fill the tank.

Therefore, the quantities are inversely proportional. In this case, when writing the proportion, we must invert one of the ratios, as shown in the diagram below:

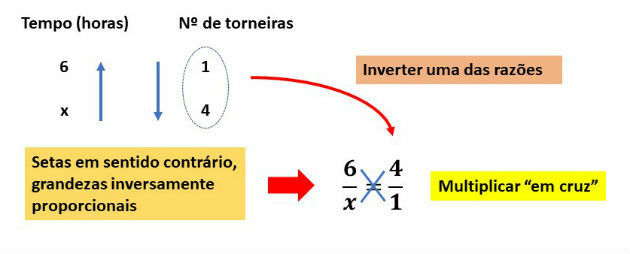
Solving the equation:

Thus, the tank will be completely full in 1.5 h.

See too: Simple and Compound Three Rule

Exercise 3

In one company, 50 employees produce 200 pieces, working 5 hours a day. If the number of employees drops by half and the number of working hours per day is reduced to 8 hours, how many parts will be produced?

Solution

The quantities indicated in the problem are: number of employees, number of parts and hours worked per day. So we have a compound rule of three (more than two quantities).

In this type of calculation, it is important to analyze separately what happens to the unknown (x), when we change the value of the other two quantities.

By doing this, we realized that the number of parts will be smaller if we reduce the number of employees, therefore, these quantities are directly proportional.

The number of parts increases if we increase the number of working hours per day. Therefore, they are also directly proportional.

In the diagram below, we indicate this fact through the arrows, which point to the increasing direction of values.

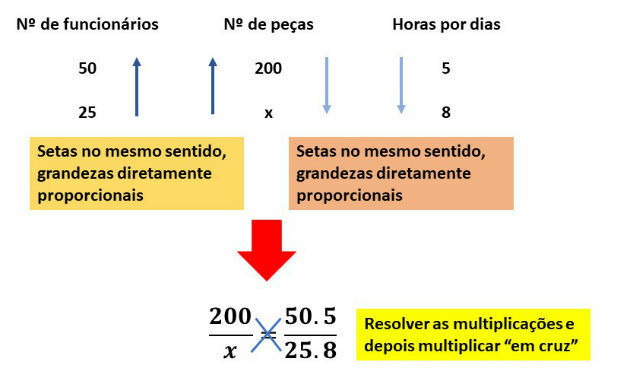
Solving the rule of three, we have:

Thus, will be produced 160 pieces.

See too: Three Compound Rule

Contest Issues Resolved

1) Epcar - 2016

Two machines A and B of different models, each maintaining its constant production speed, produce n equal parts together, taking 2 hours and 40 minutes simultaneously. Machine A working alone, keeping its speed constant, would produce, in 2 hours of operation, n/2 of these parts.

It is correct to state that machine B, keeping its production speed constant, would also produce n/2 of these parts in

a) 40 minutes.
b) 120 minutes.
c) 160 minutes.
d) 240 minutes.

See Answer

Since the total production time is 2h and 40 min, and we already know that machine A produces itself in 2 hours n/2 pieces, so let's find out how much it alone produces in the remaining 40 min. For this, let's use the rule of three.

Solving the rule of three:

This is the amount of parts produced in 40 min by machine A, so in 2 h and 40 min it alone produces:

We can then calculate the quantity produced by machine B in 2h and 40 min, subtracting the quantity produced by the two machines (n) from the quantity produced by machine A:

It is now possible to calculate how long machine B would take to produce n/2 pieces. For that, let's make a rule of three again:

Solving the rule of three, we have:

Thus, machine B will produce n/2 pieces in 240 min.

Alternative d: 240 min

See too: Magnitudes directly and inversely proportional

2) Cefet - MG - 2015

In one company, 10 employees produce 150 pieces in 30 working days. The number of employees that the company will need to produce 200 pieces, in 20 working days, is equal to

a) 18
b) 20
c) 22
d) 24

See Answer

This problem involves a compound rule of three, as we have three quantities: number of employees, number of parts and number of days.

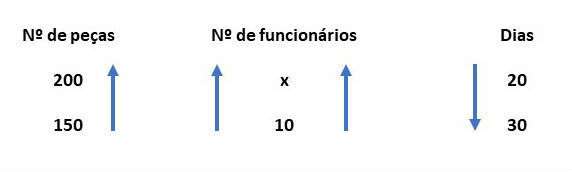
Observing the arrows, we identify that the number of parts and the number of employees are magnitudes
directly proportional. Days and number of employees are inversely proportional.
So, to solve the rule of three, we have to invert the number of days.

Soon, 20 employees will be needed.

Alternative b: 20

See too: Three Compound Rule Exercises

3) Enem - 2013

An industry has a water reservoir with a capacity of 900 m³. When there is a need to clean the reservoir, all the water needs to be drained. The drainage of water is done by six drains, and lasts 6 hours when the reservoir is full. This industry will build a new reservoir, with a capacity of 500 m³, whose water must be drained within 4 hours, when the reservoir is full. The drains used in the new reservoir must be identical to the existing ones.
The amount of drains in the new reservoir should be equal to

a) 2
b) 4
c) 5
d) 8
e) 9

See Answer

This question is a rule of three compound, being the quantities involved the capacity of the reservoir, the number of drains and the number of days.

From the position of the arrows, we observe that the capacity and the number of drains are directly proportional. The number of days and the number of drains are inversely proportional, so let's invert the number of days:

Thus, 5 drains will be needed.

Alternative c: 5

4) UERJ - 2014

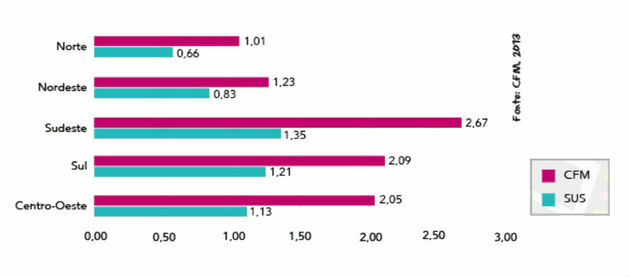
Note in the chart the number of active physicians registered with the Federal Council of Medicine (CFM) and the number number of doctors working in the Unified Health System (SUS), for every thousand inhabitants, in the five regions of Brazil.

SUS offers 1.0 doctor for each group of x inhabitants.
In the North region, the value of x is approximately equal to:

a) 660
b) 1000
c) 1334
d) 1515

See Answer

To resolve the issue, we will consider the magnitudes number of SUS physicians and the number of inhabitants in the North region. Therefore, we must remove this information from the graph presented.
Making the rule of three with the indicated values, we have:

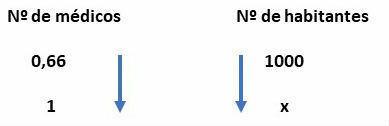
Solving the rule of three, we have:

Therefore, SUS provides approximately 1 doctor for every 1515 inhabitants in the North region.

Alternative d: 1515

See too: Simple Three Rule Exercises

5) Enem - 2017

At 5:15 pm a heavy rain starts, falling with constant intensity. A swimming pool in the shape of a rectangular parallelepiped, which was initially empty, begins to accumulate rainwater and, at 6 pm, the water level inside it reaches 20 cm in height. At that moment, the valve that releases the flow of water through a drain located at the bottom of this pool, whose flow is constant, is opened. At 6:40 pm, the rain stops and, at that exact moment, the water level in the pool dropped to 15 cm.

The moment when the water in this pool finishes draining completely is between

a) 19 h 30 min and 20 h 10 min
b) 19 h 20 min and 19 h 30 min
c) 19 h 10 min and 19 h 20 min
d) 7 pm and 7 pm 10 min
e) 18 h 40 min and 19 h

See Answer

The information tells us that in 45 min of rain, the height of the pool water rose to 20 cm. After that time, the drain valve was opened, however it continued to rain for 40 min.

Let's then calculate the height of water that was added to the pool in this time interval, using the following rule of three:

Calculating this rule of three, we have:

Now, let's calculate the amount of water that drained since the drain was opened. This amount will be equal to the sum of water that was added, minus the amount that still exists in the pool, ie:

Therefore, 205/9 cm of water has flown since the drain was opened (40 min). Now, let's calculate how long it will take to drain the amount left in the pool after it has stopped raining.

For this, let's use one more rule of three:

Calculating, we have:

Thus, the pool will be empty in approximately 26 min. Adding this value to the moment that the rain ends, it will empty at approximately 19:6 min.

Alternative d: 7 pm and 7 pm 10 min

To learn more, read also:

• Percentage
• Percentage Exercises
• Mathematics in Enem
• Exercises on Ratio and Proportion