Generally speaking, a magnetic field is defined as any region of space around a conductor carried by a current electric or around a magnet, in this case due to the particular movements that the electrons perform inside their atoms.
The magnetic induction vector can be calculated by the equation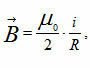 
, when it is a circular turn.
Where: B = vector induction electric field
μ = electrical permittivity constant
1) (Unicamp – SP) A homogeneous conductor with resistance 8.0 Ω has the shape of a circle. A current I = 4.0 A arrives through a straight wire at point A and leaves through point B through another perpendicular straight wire, as shown in the figure. Straight wire resistances can be considered negligible.
a) calculate the intensity of the currents in the two arcs of circumference between A and B.
b) calculate the value of the magnetic field strength B at the center O of the circle.
Solution
a) Are given in the problem:
I = 4.0A
R = 8.0 Ω
The following figure schematically represents the problem statement:
With 8.0 Ω, the resistance across the entire circumference, we conclude that the section corresponding to 1/4 of the circumference has resistance:
R1 = 2,0 Ω
And the other stretch, corresponding to 3/4 of the circumference has resistance
R2 = 6,0 Ω
As the potential difference is equal for each resistor, we have:
U1 = U2
R1.i1 = R2.i2
2.0.i1 = 6.0.i2
i1 = 3.0.i2
the current I arrives by the thread at point A and divides into i1 Hey2, thus:
i = i1 + i2, knowing that I = 4.0 A is that i1= 3.0.i2, We have to:
4.0 = 3.0i2 + i2
4.0 = 4.0.i2
i2 = 1.0 A
Therefore,
i1 = 3.0A
b) the electric current i1 originates in the center O a field B1, entering the screen 
(Right hand rule). 
The electric current i2 originates in the center O a field B2, leaving the screen 
(Right hand rule).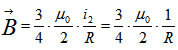 
We can conclude then that B1 = B2, so the resulting field is
Resultant = 0
2) Two equal turns, each with a radius of 2π cm, are placed with coincident centers in perpendicular planes. Being traversed by currents i1 = 4.0 A and i2 = 3.0 A, characterize the resulting magnetic induction vector at its center O. (Given: μ0 = 4μ. 10-7 T.m/A).
The magnetic field generated by current i1 = 4.0 A in turn 1 is: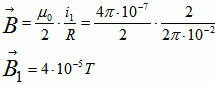 
The field generated by current i2 = 3.0 A in turn 2 is: 
As the spirals are arranged perpendicularly, the resulting field is: 
By Kléber Cavalcante
Graduated in Physics
Brazil School Team
Electromagnetism - Physics - Brazil School
Source: Brazil School - https://brasilescola.uol.com.br/fisica/exercicios-resolvidos-campo-magnetico-uma-espira-circular.htm
