mirrorsspherical are optical systems formed on the basis of hubcapspolishedand reflectors, able to reflect the light at different angles, thus producing images that can both be real as virtual. There are two types of spherical mirrors: mirrorsconcave and the mirrorsconvex. Before delving into the details of each of these mirrors, let's identify and define what the elementsgeometricFrommirrorsspherical.
Lookalso:Discover the most incredible optical phenomena
Geometric elements of spherical mirrors
The geometric elements of spherical mirrors are very useful for your analytical study, through the geometric optics. Regardless of the shapes of the spherical mirror (concave or convex), these elements are the same for both.
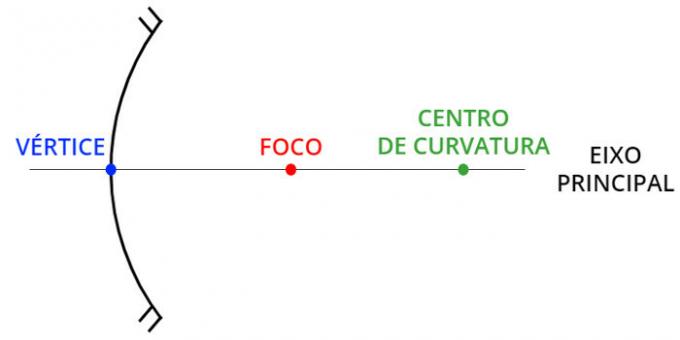
Vertex (V)
O vertex marks the central region of the spherical mirrors. It is at this point that we draw the main axis (or symmetry axis) of the mirror. Any light beam that focuses on the vertex of a spherical mirror is reflected with the same angle of incidence, just as a flat mirror would.
Center of curvature (C)
O center of curvature of the spherical mirrors is the Scoremedium of the spherical cap that gives rise to the mirror, therefore, it is equal to the Ray of that sphere. Any ray of light that falls on the center of curvature of a spherical mirror must be reflected on itself, so that the incident and reflected light rays travel the same path.
radius of curvature (R)
O radius of curvature measures the distance between the vertex from the mirror and yours center ofcurvature, it is denoted by the letter R and is commonly measured in meters.
See too: What is the speed of light?
Focus (F)
O focus is the point where parallel light rays converge after being reflected by a mirrorconcave. In the case of mirrors convex, the reflected light rays diverge of its surface and, therefore, are the extensions of light rays that intersect, at a point located "behind" the surface of these mirrors. For this reason, we say that the focus of convex mirrors is virtual, while the focus of the concave mirrors is real.
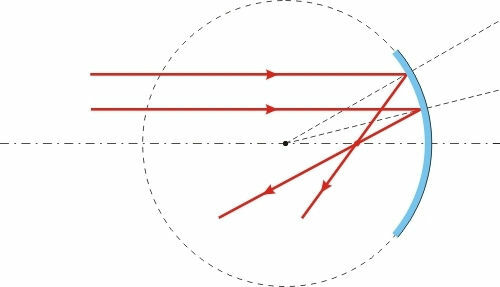
The type of mirror focus directly influences the calculation. mirrors with real focus (concave) have their focal point written with the signalpositive, the convex mirrors receive the signalnegative for your focus:
concave mirror |
Real focus, plus sign, in front of the mirror |
convex mirror |
Virtual focus, minus sign, behind mirror |
The figure shown below represents the reflection of light by a mirrorconvex. Realize that the reflected light rays are divergent, in this case, what happens is the crossing of the extensions of light rays, that's why the image conjugated by these mirrors appears behind of the reflective surface:

Focal length (f)
THE focal distance measures the position of the focus in relation to the vertex of the spherical mirrors, in addition, parallel light rays that focus on concave mirrors are reflected on the focal point. In the case of convex mirrors, they are the extensions of light rays that cross in their focus, located behind the mirror, called virtual focus.
Opening angle
The opening angle measures the degree ofcurvature of the mirror. This angle is measured from the axis of symmetry of the spherical mirrors. The larger the opening angle, the more the mirror resembles a flat mirror.
concave mirrors
You mirrorsconcave are cavities constant ray reflectors. are used to produce virtual and enlarged images of objects positioned in regions close to its surface, as in the case of mirrors used in optics or for applying makeup, etc. This type of mirror is also able to conjugate real and therefore inverted images, when positioning an object beyond its focal length.
In order to better understand how concave mirrors conjugate images, we will need to describe each of the possible cases. Note that the situations described below are in order of distance from the vertex of the mirror, check:
Case 1 - Object positioned between the vertex and the focus of the concave mirror
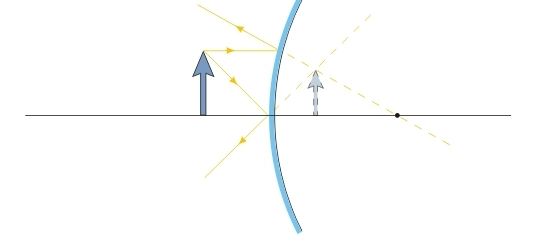
When placing an object between the vertex and focus of a concave mirror, the latter will produce a Imagevirtual of the object, "behind” of the mirror surface. The reflected light rays are divergent, therefore, their extensions intersect, forming an enlarged image of the object.

Case 2 - Object positioned over the concave mirror focus
When any object is positioned exactly over the concave mirror's focal point, it does not match Imagenone, since neither the reflected rays nor their extensions intersect. In this case, we say the image is improper or that is formed in the infinite.
Case 3 - Object positioned between focus and center of curvature
When placing any object between the focus and the center of curvature of a convex mirror, the image produced will always be real (therefore inverted) and bigger than the object.
Case 4 - Object positioned on the center of curvature
When any object is placed at a distance from the center of curvature in relation to the vertex of the concave mirror, it combines a Imagereal It's from samesize of your object.
Case 5 - Object positioned beyond the center of curvature
Objects that are positioned beyond the center of curvature produce imagesreal and minors than your objects.
in short
Concave mirrors produce real images when we place objects close to their surface, at focal distance there is no formation image, beyond the focus, the images are real and their size decreases according to the distance between the object and the vertex of the mirror.
Lookalso:Discover the main optical instruments
convex mirrors
You mirrorsconvex are like the surfaceexternal of a reflective cap. These mirrors only combine virtual images, which are those which are formed behind the mirrors and can be seen thanks to an optical illusion. This type of image will always be mated in the same orientation (face up or down) as your objects.
In addition to these features, regardless of the position of the image object, the images conjugated by the convex mirrors will always be smaller than their objects. Convex mirrors are widely used in commercial establishments and also in public transport thanks to the large visual field that this type of mirror is capable of providing.
in short
Convex mirrors only produce virtual (direct) and reduced images, regardless of the distance between the object and the vertex of the mirror
Formulas on spherical mirrors
The formulas used for the analytical study of spherical mirrors apply to both concave and convex mirrors. The main difference between this type of mirror is the algebraic sign which is assigned to focus (f).
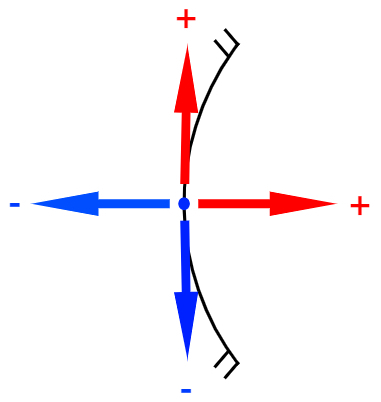
mirrorsconvex, which feature virtual focus, feature focusnegative, while the mirrorsconcave, whose focuses are real, they present focuspositive. Furthermore, it is important to define a referential for the use of algebraic signs, for that, the Gauss referential is used. According to Gaussian referential:
Any object or image that is in front of the mirror's reflecting surface must receive a positive signal.
Any object or image that lies behind the mirror's reflecting surface must receive a negative signal.
Any object or image that has a vertical upward orientation must receive a positive sign.
Any object or image that has a vertical downward orientation must receive a negative sign.
The figure below shows a small scheme to facilitate the understanding of the signals used according to the Gaussian framework:
we denote by the letter for the position of objects in relation to the vertex of the mirrors. The position of the images conjugated by the mirrors, in turn, is denoted by the letter for'. In possession of these statements, let us go to the formulas.
Focal length and radius of curvature
There is a formula valid for all spherical mirrors that relates the focal length to the radius of curvature, check it out:
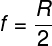
f - focal distance
R - radius of curvature
Equation of Conjugated Points or Gaussian Equation
The equation of conjugate points relates the focal length (f), the object position (p) and the image position (p'), both measured in relation to the mirror vertex, see:
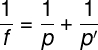
f - focal distance
for - object position
for' - image position
Transverse linear increase equation
Transverse linear magnification is the dimensionless quantity (without measurement unit) that measures the relationship between the size of the object and that of its image combined by spherical mirrors. There are three different ways to calculate the transverse linear increase, check it out:
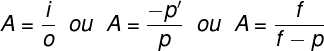
THE - transverse linear increase
i - image size
O - object size
f - focal distance
To better understand the meaning of transversal linear increase, check out some possible results and their interpretations:
A = 1: in this case, the image is the same size as the object and its orientation is positive (virtual image);
A = -1: in this case, the image is the same size as the object, however it is inverted (real image);
A = + 0.5: virtual image (right) half the size of the object;
A = - 2.5: real (inverted) image 2.5 times the size of the object.
Lookalso:What color is the water?
Solved exercises on spherical mirrors
1) An object is placed 50 cm in front of a concave mirror whose focal length is 25 cm. Determine in which position the image of this object is formed.
a) - 50 cm
b) +50 cm
c) + 25 cm
d) - 40 cm
e) + 75 cm
Feedback: Letter B
Resolution:
To solve this exercise, you will need the Gauss equation, observe the calculations:
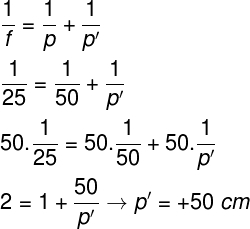
In the previous calculation, we tried to calculate p', the position of the image. To do this, we substitute the focus and position data of the object in the Gauss equation, resulting in a position of 50 cm in front of the mirror. Thus, the correct alternative is the letter B.
2) A 10 cm high object is placed 30 cm from a convex mirror whose focal length is -10 cm. Determine the size of the image conjugated by this mirror.
a) - 5 cm
b) - 10 cm
c) - 25 cm
d) - 50 cm
e) - 100 cm
Feedback: Letter a
Resolution:
To solve this exercise, we will make use of the transversal linear increase equation, check the calculation to be done:
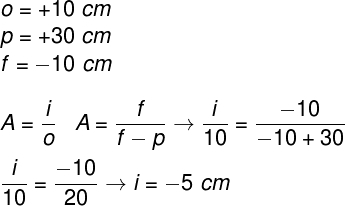
To solve this exercise, we used two of the three formulas used to calculate the transverse linear increase, resulting in an image of -5 cm. This indicates that the image is reduced relative to the object and inverted, therefore real.
3) It is common to use concave mirrors in optics, so that it is possible to examine details of the frames, thanks to the formation of images larger than their objects. In order for a concave mirror to form direct and larger images than its objects, it is necessary to position the object
a) between the focus and the center of curvature.
b) between apex and focus.
c) beyond the center of curvature.
d) beyond focus.
e) about the focus.
Feedback: Letter B
Resolution:
There is only one case in which concave mirrors are able to conjugate virtual (direct) images: when some object is positioned close to its surface, at distances smaller than the focal length of the mirror. Therefore, the correct alternative is the letter B.
By Me. Rafael Helerbrock
Source: Brazil School - https://brasilescola.uol.com.br/fisica/espelhos-esfericos.htm

