conical are plane geometric figures defined from the intersection of a double cone of revolution with a plane. The figures that can be obtained at this intersection, and that can be called conics, are: circumference, Ellipse, parable and hyperbole.
O conedouble in revolution is achieved by rotating a line r about an axis, which, in turn, is another line concurrent with the straight a. The following image shows the straight line that was rotated, the axis and the figure obtained from this revolution.

All definitions of conical are based on distance between two points, which can be found in the plan through the Pythagorean theorem.
Circumference
Given a point C and a fixed length r, every point that is within a distance r of point C is a point on the circle. Point C is called the center of the circumference and r is its radius. The following image shows an example of a circle and the shape it takes on the Cartesian plane:

Given the coordinates of point C (a, b), the coordinates of point P (x, y) and the length of the segment r, the reduced equation of circumference é:
(x - a)2 + (y – b)2 = r2
Ellipse
Given two points F1 and F2 of the plane, called focuses, a Ellipse is the set of points P, such that the sum of the distance from P to F1 with the distance from P to F2 is the 2a constant. The distance between the F points1 and F2 is 2c and 2a > 2c.
Comparing the definitions of Ellipse and circumference, in the ellipse, we add the distances that go from a point of the ellipse to its focuses and observe the constant result. On the circumference, only one distance is constant.
The following image shows an example of Ellipse and the shape of this figure in the Cartesian plane:

In this figure, you can see the segments a, b and c, which will be used to determine the equationsreduced gives Ellipse.
There are two versions of the reduced equation of Ellipse; the first is valid for when the foci are on the x-axis of a Cartesian plane and the center of the ellipse coincides with the origin:
x2 + y2 = 1
The2 B2
The second version is valid for when the focuses are on the y axis and the center of the ellipse coincides with the origin:
y2 + x2 = 1
The2 B2
Parable
Given a line r, called the guideline, and a point F, called the focus, both belonging to the same plane, a parable is the set of points P, such that the distance between P and F is equal to the distance between P and r.
The following figure shows an example of a parable:
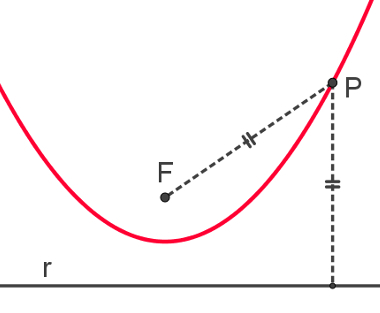
The parameter of a parable and the distance between the focus and the guideline, and this measure is represented by the letter p. There are also two versions of the reduced equation of the parabola. The first is valid when the focus is on the x-axis:
y2 = 2px
The second is valid when the focus is on the y axis:
x2 = 2py
Hyperbole
Given two distinct points F1 and F2, called focuses, of any plane, and the distance 2c between these points, a point P will belong to the hyperbole if the difference between the distance from P to F1 and the distance from P to F2, in modulus, is equal to a constant 2a. Thus:
|PF1 - FEDERAL POLICE2| = 2nd
The following image is a hyperbole with segments a, b and c.

Hyperbole also has two versions of the reduced equation. The first concerns the cases where the F points1 and F2 are on the x-axis and the center of the hyperbole it is the origin of the Cartesian plane.
x2 - y2 = 1
The2 B2
The second case is when the focuses gives hyperbole they are on the y axis and their center coincides with the origin of the Cartesian plane.
y2 - x2 = 1
The2 B2
By Luiz Paulo Moreira
Graduated in Mathematics
Source: Brazil School - https://brasilescola.uol.com.br/o-que-e/matematica/o-que-sao-conicas.htm
