Cartographic scale is the ratio of area reduction of the actual landscape to its representation on the map. This value is necessary because the reproduction is not random, but proportional.
In other words, the cartographic scale is a value used to represent distances from the real landscape on the paper.
Scale helps us understand maps and understand measurements between represented territories.
There are two types of cartographic scales: numerical and graphical.
The numerical scale expresses the value in numbers, while the graph uses both numbers and a horizontal line.
numerical scale
The numerical scale is the representation of the proportions between the real landscape and the map through numbers.
Example: 1:100,000.
We will always find three elements in the numerical cartographic scale:
- the number 1
- two points
- a variant number whose measurement is ever in centimeters.
So we have:
1:100.000
If we were to write with words we would say:
“One centimeter on the map means 1 kilometer in the real landscape”.
After all, 100,000 centimeters equals one kilometer.
How to calculate the numerical scale?
To calculate the numerical scale we need to apply the rule of three and convert the requested measures. In this case, we will transform centimeters into kilometers and vice versa.
Let's look at the following example:
On a map, a road is 6 (six) centimeters and the scale indicates 1:350,000. How long is the road in the real landscape?
For this, we use the formula:
AND: Scale
d: distance measured on the map
D: distance in reality
We use the rule of three, where:
Number 1 will equal 350,000 centimeters.
The number 6 corresponds to the distance on the map (d).
X will be the value we want to find (D).
So we'll multiply 6 times 350,000 to get the value of X.
Mathematically, we can express it this way:
After that, we multiply:
Answer: 2,100,000 centimeters.
The next step will be to transform this value in centimeters to kilometers.
See too: Units of Measure
Graphic scale
The graphic scale is a representation used on maps to express measurements. It is a horizontal line, with white and black rectangles, which indicates the values expressed on the map equivalent to the real landscape.
In the graphic scale we need to observe what the expressed values are. Each centimeter of the scale will correspond to a certain distance, expressed in meters or kilometers.
Thus, we have:
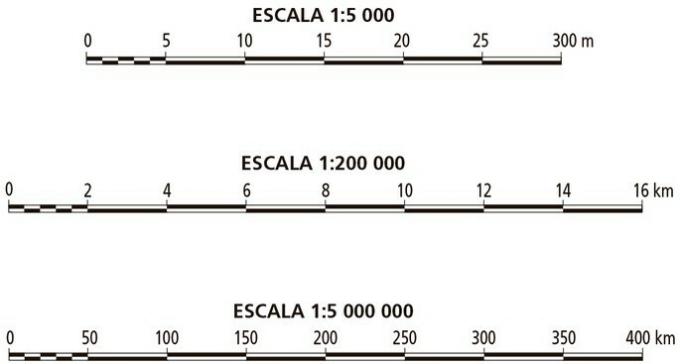
On the first scale there is the numerical value: 1: 5 000
This means that every 1 centimeter on this scale will be equivalent to 5000 centimeters in the real landscape. If we make the conversion, we have that 5 000 centimeters equals 50 meters.
On the second scale there is a numerical value: 1:200 000.
This means that every 1 centimeter on this scale will be equivalent to 200 000 centimeters in the real landscape. If we make the conversion, we have that 200 000 centimeters equals 2 kilometers.
On the third scale there is the numerical value: 1: 5 000 000
This means that every 1 centimeter on this scale will be equivalent to 5,000,000 centimeters in the real landscape. If we do the conversion, we have that 5000 centimeters equals 50 kilometers.
Numerical Scale Exercises
Question 1 (Mackenzie)
Considering that the real distance between two cities is 120 km and that its graphic distance on a map is 6 cm, we can say that this map was projected at scale:
a) 1: 1 200 000
b) 1: 2,000,000
c) 1: 12,000,000
d) 1: 20,000,000
e) 1: 48,000,000
Correct alternative: b) 1: 2,000,000
Using the formula:
Where:
E: Scale
d: distance measured on the map (cm)
D: distance in reality (cm)
Remember that to perform the calculations we must always leave all data with the same unit of measure, which in numerical scale must be centimeters.
To transform the actual distance of 120 km into centimeters, we must remember that 1 km has 100,000 cm, because:
Thus, 120 km has:
The scale must always start with 1, so we divide the numerator and denominator by 6 to simplify the answer and get the number 1 in the numerator.
So the final answer is 1:2 000 000.
Question 2 (Mackenzie)
A road is 13 kilometers in a straight line. When represented on a 1:500,000 scale map, how big is the representation in centimeters?
a) 65
b) 20.6
c) 26
d) 0.26
e) 2.6
Correct alternative: e) 2.6
Scaling formula:
Where:
E: Scale
d: distance measured on the map (cm)
D: distance in reality (cm)
Then:
In the statement, the scale is 1:500 000:
Putting it in the formula, it's:
Remember that we must always leave the data with the same measurement unit, scale uses centimeters, so we need to transform 13 km into centimeters.
After turning 13 km, we have 1,300,000 centimeters, so:
So we have, that 2.6 cm is the distance that will be found on the map.
3. (UFJF/2001) The distance between two points on a map measures 20 millimeters. Using the scale of this map we find the real distance of 100 km. The scale of this map is:
a) 1: 5,000,000
b) 1: 200 000
c) 1: 100,000
d) 1: 50 000
Correct alternative: a) 1: 5,000,000
Scaling formula:
Where:
E: Scale
d: distance measured on the map (cm)
D: distance in reality (cm)
Note that in the statement the measurement units are different, we have millimeters and kilometers. In scaling we must always transform everything to centimeters.
The actual distance is 10,000,000 cm, as
In scale, the final numerator must always be 1, so we can simplify the numerator and denominator by 2.
So the scale is 1: 5 000 000
We have more texts on cartographic scale for you:
- What is cartography?
- Cartographic Scale Exercises


