Exponential Function: 5 commented exercises

THE exponential function is every function of ℝ in ℝ^*_+, defined by f(x) = a^x, where a is a real number, greater than zero and not equal to 1.

Take advantage of the exercises commented to clear all your doubts about this content and be sure to check your knowledge in the resolved questions of contests.

Commented Exercises

Exercise 1

A group of biologists is studying the development of a particular colony of bacteria and found that under ideal conditions, the number of bacteria can be found through the expression N(t) = 2000. 2^0.5t, being t in hours.

Considering these conditions, how long after the start of observation will the number of bacteria equal 8192000?

Solution

In the proposed situation, we know the number of bacteria, that is, we know that N(t) = 8192000 and we want to find the value of t. So, just replace this value in the given expression:

To solve this equation, let's write the number 4096 in prime factors, because if we have the same base, we can equal the exponents. Therefore, factoring the number, we have:

Thus, the culture will have 8 192 000 bacteria after 1 day (24 h) from the start of the observation.

Exercise 2

Radioactive materials have a natural tendency, over time, to disintegrate their radioactive mass. The time it takes for half of its radioactive mass to disintegrate is called its half-life.

The amount of radioactive material of a given element is given by:

Being,

N(t): the amount of radioactive material (in grams) in a given time.
N₀: the initial amount of material (in grams)
T: half-life time (in years)
t: time (in years)

Considering that the half-life of this element is equal to 28 years, determine the time needed for the radioactive material to reduce to 25% of its initial amount.

Solution

For the proposed situation A(t) = 0.25 A₀ = 1/4 A₀, so we can write the given expression, replacing T by 28 years, then:

Therefore, it will take 56 years for the amount of radioactive material to be reduced by 25%.

Contest Questions

1) Unesp - 2018

Ibuprofen is a prescribed medication for pain and fever, with a half-life of approximately 2 hours. This means that, for example, after 2 hours of ingesting 200 mg of ibuprofen, only 100 mg of the medication will remain in the patient's bloodstream. After another 2 hours (4 hours in total), only 50 mg will remain in the bloodstream and so on. If a patient receives 800 mg of ibuprofen every 6 hours, the amount of this medication that will remain in the bloodstream for the 14th hour after taking the first dose will be

a) 12.50 mg
b) 456.25 mg
c) 114.28 mg
d) 6.25 mg
e) 537.50 mg

See Answer

As the initial amount of medication in the bloodstream every 2 hours is divided in half, we can represent this situation using the following scheme:

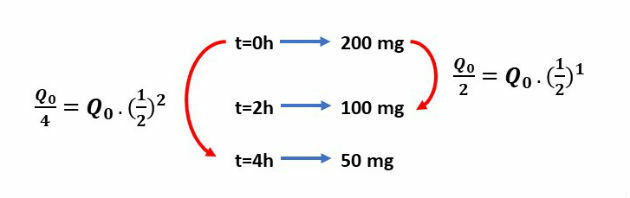
Note that the exponent, in each situation, is equal to time divided by 2. Thus, we can define the amount of medication in the bloodstream as a function of time, using the following expression:

Being

Q(t): the quantity in a given hour
Q₀: the initial amount ingested
t: time in hours

Considering that 800 mg of ibuprofen were taken every 6 h, then we have:

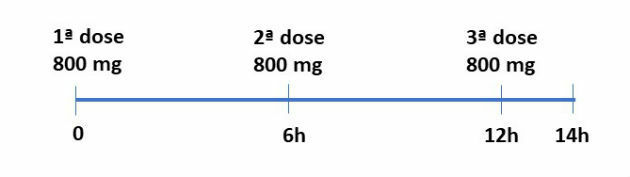
To find the amount of medication in the bloodstream 14 hours after ingesting the 1st dose, we must add the amounts referring to the 1st, 2nd and 3rd doses. Calculating these quantities, we have:

The amount of the 1st dose will be found considering the time equal to 14 h, so we have:

For the second dose, as shown in the diagram above, the time was 8 hours. Replacing this value, we have:

The time for the 3rd dose will be only 2 hours. The amount related to the 3rd dose will then be:

Now that we know the amounts for each dose ingested, we can find the total amount by adding each of the amounts found:

Q_total= 6.25 + 50 + 400 = 456.25 mg

Alternative b) 456.25 mg

2) UERJ - 2013

A lake used to supply a city was contaminated after an industrial accident, reaching the level of toxicity T₀, corresponding to ten times the initial level.
Read the information below.

• The lake's natural flow allows 50% of its volume to be renewed every ten days.
• The toxicity level T(x), after x days of the accident, can be calculated using the following equation:

Consider D the smallest number of days of suspension of the water supply, necessary for the toxicity to return to the initial level.
If log 2 = 0.3, the value of D is equal to:

a) 30
b) 32
c) 34
d) 36

See Answer

To return to the initial toxicity level it is necessary that:

Substituting this value in the given function, we have:

Multiplying in "cross", the equation becomes:

2 ^0.1x= 10

Let's apply the base 10 logarithm to both sides to turn it into a 1st degree equation:

log (2^0.1x) = log 10

Remembering that the log of 10 in base 10 is equal to 1, our equation will look like:

0.1x. log 2 = 1

Considering that log 2 = 0.3 and substituting this value in the equation:

Thus, the smallest number of days, approximately, that supply should be suspended is 34 days.

Alternative c) 34

3) Fuvesp - 2018

Let f: ℝ → ℝ and g: ℝ₊ →ℝ defined by

respectively.

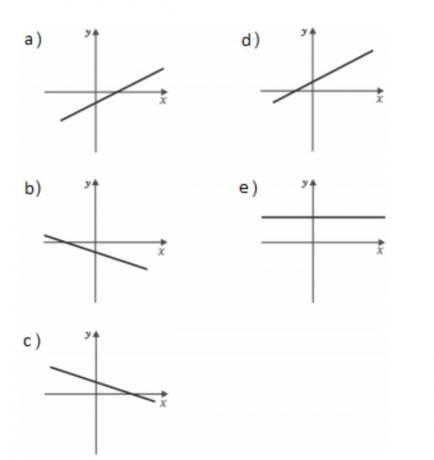
The graph of the composite function g_ºfaith:

See Answer

The graph you are looking for is the composite function g_ºf, therefore, the first step is to determine this function. For this, we must replace the function f (x) in the x of the function g (x). By making this replacement, we will find:

Using the logarithm property of the quotient and a power, we have:

Note that the function found above is of type ax+b, which is an affine function. So your graph will be a straight line.

Also, the slope a is equal to log₁₀ 5, which is a positive number, so the graph will be increasing. In this way, we can eliminate options b, c and e.

We are left with options a and d, however, when x=0 we have gof = - log₁₀ 2 which is a negative value as represented in graph a.

Alternative a)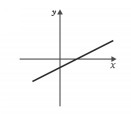

4) Unicamp - 2014

The graph below shows the biotic potential curve q (t) for a population of microorganisms over time t.

Since a and b are real constants, the function that can represent this potential is

a) q(t) = at + b
b) q(t) = ab^t
c) q(t) = at² + bt
d) q(t) = a + log _B t

See Answer

From the graph shown, we can identify that when t=0, the function is equal to 1000. Furthermore, it is also possible to observe that the function is not affine, as the graph is not a straight line.

If the function were of type q (t) = at²+bt, when t = 0, the result would be equal to zero and not 1000. So it's not a quadratic function either.

How to log_B0 is not defined, nor could it have as an answer the function q (t) = a + log_Bt.

Thus, the only option would be the function q(t) = ab^t. Considering t=0, the function will be q (t) = a, as a is a constant value, it is enough that it is equal to 1000 for the function to fit the given graph.

Alternative b) q (t) = ab^t

5) Enem (PPL) - 2015

The workers union of a company suggests that the salary floor of the class be R$ 1,800.00, proposing a fixed percentage increase for each year dedicated to work. The expression that corresponds to the salary proposal (s), as a function of length of service (t), in years, is s (t) = 1800. (1,03)^t .

According to the union's proposal, the salary of a professional from this company with 2 years of service will be, in reais,

a) 7 416.00
b) 3,819.24
c) 3,709.62
d) 3,708.00
e) 1,909.62.

See Answer

The expression for calculating the wage as a function of time proposed by the union corresponds to an exponential function.

To find the salary value in the indicated situation, let's calculate the value of s, when t=2, as indicated below:

s(2) = 1800. (1,03)² = 1800. 1,0609 = 1 909,62

Alternative e) 1 909.62

Read too:

• Exponential Function
• Logarithm
• Logarithm - Exercises
• Logarithm Properties
• Potentiation
• potentiation exercises
• Affine Function
• Linear Function
• Related Function Exercises
• Quadratic Function
• Quadratic Function - Exercises
• Math Formulas