Common Concentration: exercises with commented feedback

Common concentration is the amount of solute, in grams, in 1 liter of solution.

Mathematically, the common concentration is expressed by:

1. (Mackenzie) What is the concentration, in g/L, of the solution obtained by dissolving 4 g of sodium chloride in 50 cm³ of water?

a) 200 g/L
b) 20 g/L
c) 0.08 g/L
d) 12.5 g/L
e) 80 g/L

See Answer

Correct alternative: e) 80 g/L.

1st step: Transform the volume unit of cm³ to L.

Knowing that 1 cm³ = 1 mL, then we have:

Step 2: Apply the data in the common concentration formula:

2. (Mackenzie) There are five containers containing aqueous solutions of sodium chloride.

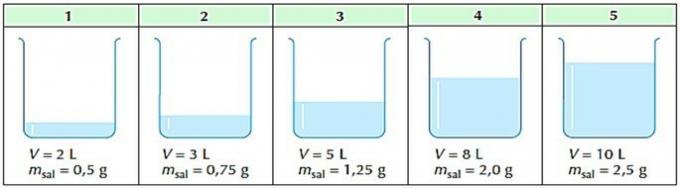
It is correct to say that:

a) container 5 contains the least concentrated solution.
b) container 1 contains the most concentrated solution.
c) only containers 3 and 4 contain solutions of equal concentration.
d) the five solutions have the same concentration.
e) container 5 contains the most concentrated solution.

See Answer

Correct alternative: d) the five solutions have the same concentration.

Applying the Common Concentration Formula for each of the containers, we have:

1	2	3	4	5

From the calculations performed, we see that all solutions have the same concentration.

3. (UFPI) The new traffic legislation provides for a maximum limit of 6 decigrams of alcohol, C₂H₅OH, per liter of blood from the driver (0.6 g/L). Considering that the average percentage of alcohol ingested that remains in the blood is 15% by mass, identify, for an adult with an average weight of 70 kg whose blood volume is 5 liters, the maximum number of beer cans (volume = 350 mL) ingested without the established limit being outdated. Additional information: the beer has 5% alcohol by volume, and the alcohol density is 0.80 g/mL.

to 1
b) 2
c) 3
d) 4
e) 5

See Answer

Correct alternative: a) 1.

Question data:

• Maximum allowed blood alcohol limit: 0.6 g/L
• Percentage of ingested alcohol remaining in the blood: 15%
• Blood volume: 5 L
• Beer can volume: 350 mL
• Percentage of alcohol in beer: 5%
• Alcohol density: 0.80 g/mL

1st step: Calculate the mass of alcohol in 5 L of blood.

2nd step: Calculate the total alcohol mass, as only 15% was absorbed into the bloodstream.

3rd step: Calculate the volume of alcohol present in the beer.

Step 4: Calculate the maximum volume of beer that can be consumed.

5th step: Interpretation of results.

The maximum volume of beer that a person can drink so that the concentration of alcohol in the blood does not exceed 0.6 g/L is 500 ml.

Each beer contains 350 mL and when consuming two cans, the volume is 700 mL, which exceeds the established volume. As such, the most a person can ingest is one can.

4. (UNEB) The homemade serum consists of an aqueous solution of sodium chloride (3.5 g/L) and sucrose (11 g/L). The masses of sodium chloride and sucrose needed to prepare 500 ml of homemade serum are, respectively:

a) 17.5 g and 55 g
b) 175 g and 550 g
c) 1750mg and 5500mg
d) 17.5 mg and 55 mg
e) 175 mg and 550 mg

See Answer

Correct alternative: c) 1750mg and 5500mg.

Calculate the mass of sodium chloride

1st step: Transform the volume unit from mL to L.

2nd step: Calculate the mass in grams.

3rd step: Transform the found value to milligrams.

Calculate the mass of sucrose

1st step: Calculate the mass in grams.

Knowing that 500 mL = 0.5 L, then we have:

2nd step: Transform the found value to milligrams.

5. (PUC-Campinas) Totally evaporate the solvent from 250 ml of an aqueous MgCl solution₂ of concentration 8.0 g/L. How many grams of solute are obtained?

a) 8.0
b) 6.0
c) 4.0
d) 2.0
e) 1.0

See Answer

Correct alternative: d) 2.0.

1st step: Transform the volume unit from mL to L.

2nd step: Calculate the mass of magnesium chloride (MgCl₂).

6. (Mackenzie) The mass of the four main salts that are dissolved in 1 liter of sea water is equal to 30 g. In a marine aquarium, containing 2.10⁶ cm³ of this water, the amount of salts dissolved in it is:

a) 6.0. 10¹ kg
b) 6.0. 10⁴ kg
c) 1.8. 10² kg
d) 2.4. 10⁸ kg
e) 8.0. 10⁶ kg

See Answer

Correct alternative: a) 6.0. 10¹ kg.

1st step: Calculate the mass of dissolved salts in the aquarium.

Knowing that 1 L = 1000 mL = 1000 cm³, we have:

Step 2: Transform mass unit from grams to kilograms.

3rd step: Transform the result to scientific notation.

As a number in scientific notation it has the format N. 10^no, to turn 60 kg into scientific notation we "walk" with the comma and place it between 6 and 0.

We have N = 6.0 and since we are only walking one decimal place, the value of n is 1 and the correct answer is: 6.0. 10¹ kg.

7. (UFPI) An analgesic in drops must be administered in amounts of 3 mg per kilogram of body mass, however, it cannot exceed 200 mg per dose. Knowing that each drop contains 5 mg of analgesic, how many drops should be given to a 70 kg patient?

See Answer

Correct answer: 40 drops.

Question data:

• Recommended analgesic dose: 3 mg/kg
• Amount of analgesic in drop: 5 mg of analgesic
• patient weight: 70 kg

1st step: Calculate the amount of analgesic according to the patient's weight.

The calculated amount exceeds the maximum dose. Therefore, 200 mg must be administered, which corresponds to the permitted limit.

2nd step: Calculate the amount of analgesic drop.

8. (Enem) A certain station treats about 30 000 liters of water per second. To avoid the risk of fluorosis, the maximum concentration of fluorides in this water should not exceed about 1.5 milligrams per liter of water. The maximum amount of this chemical species that can be safely used, in the volume of water treated in one hour, at this station, is:

a) 1.5 kg
b) 4.5 kg
c) 96 kg
d) 124 kg
e) 162 kg

See Answer

Correct alternative: e) 162 kg.

Question data:

• Treated water: 30,000 L/s
• Fluoride concentration: 1.5 mg/L

1st step: Transform hour into minutes.

2nd step: Calculate fluoride mass in 30000 L/s.

3rd step: Calculate the mass for the time of 1 h (3600 s).

4th step: Transform the unit of mass from mg to kg.

9. (UFRN) One of the economic potentials of Rio Grande do Norte is the production of sea salt. Sodium chloride is obtained from sea water in salt pans built near the coast. In general, sea water travels through several crystallization tanks up to a determined concentration. Suppose that, in one of the steps of the process, a technician took 3 samples of 500 mL from a crystallization, carried out evaporation with each sample and noted the resulting salt mass in table a follow:

Sample	Sample volume (mL)	Salt mass (g)
1	500	22
2	500	20
3	500	24

The average concentration of the samples will be:

a) 48 g/L
b) 44 g/L
c) 42 g/L
d) 40 g/L

See Answer

Correct alternative: b) 44 g/L.

1st step: Transform the volume unit from mL to L.

Step 2: Apply the common concentration formula for each of the samples.

1	2	3

3rd step: Calculate the average concentration.

10. (Fuvest) Consider two cans of the same soda, one in the “diet” version and the other in the common version. Both contain the same volume of liquid (300 mL) and have the same mass when empty. The composition of the refrigerant is the same in both, except for one difference: the common version contains a certain amount of sugar, while the “diet” version does not contain sugar (only negligible mass of a sweetener artificial). By weighing two closed soda cans, the following results were obtained:

Sample	Mass (g)
Can with regular soda	331.2 g
Can with "diet" soda	316.2 g

Based on these data, it can be concluded that the concentration, in g/L, of sugar in regular soft drinks is approximately:

a) 0.020
b) 0.050
c) 1.1
d) 20
e) 50

See Answer

Correct alternative: e) 50.

1st step: Calculate the sugar mass.

As the only difference between soft drinks is the mass of sugar, as it is only present in the common version, we can find it by subtracting the masses given from each sample.

2nd step: Transform the volume unit from mL to L.

3rd step: Calculate the sugar concentration.

To gain more knowledge about chemical solutions, see also these texts.:

• Solute and solvent
• Dilution of solutions
• Molarity
• Molality