Vectors are arrows that have direction, magnitude and direction as characteristics. In physics, in addition to these characteristics, vectors have names. This is because they represent magnitudes (force, acceleration, for example). If we are talking about the acceleration vector, an arrow (vector) will be above the letter a.
Horizontal direction, magnitude and direction (left to right) of the acceleration vector
sum of vectors
The addition of vectors can be done through two rules, following the steps below:
Parallelogram Rule
1st Join the vector origins.
2nd Draw a line parallel to each of the vectors, forming a parallelogram.
3.º Add the diagonal of the parallelogram.
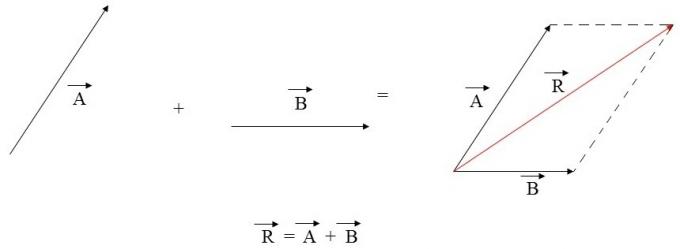
It should be noted that in this rule we can only add 2 vectors at a time.
Polygonal Rule
1st Join the vectors, one by the origin, the other by the end (tip). Do this successively, according to the number of vectors you need to add.
2nd Draw a perpendicular line between the origin of the 1st vector and the end of the last vector.
3rd Add the perpendicular line.
It should be noted that in this rule we can add several vectors at a time.
vector subtraction
The vector subtraction operation can be done by the same rules as addition.
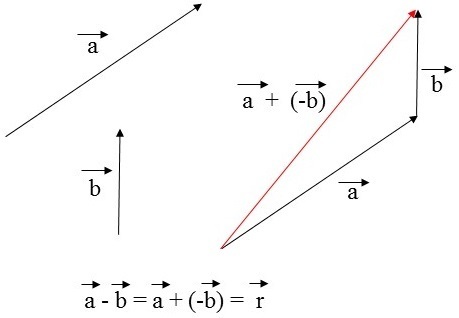
Parallelogram Rule
1st Make lines parallel to each of the vectors, forming a parallelogram.
2nd Next, make the resulting vector, which is the vector that is on the diagonal of this parallelogram.
3. Do the subtraction, considering that A is the opposite vector of -B.
Polygonal Rule
1st Join the vectors, one by the origin, the other by the end (tip). Do this successively, according to the number of vectors you need to add.
2nd Make a perpendicular line between the origin of the 1st vector and the end of the last vector.
3rd Subtract the perpendicular line, considering that A is the opposite vector of -B.
Vector Decomposition
In the vector decomposition through a single vector we can find the components in two axes. These components are the sum of two vectors that result in the initial vector.
The parallelogram rule can also be used in this operation:
1st Draw two axes perpendicular to each other, originating from the existing vector.
2nd Draw a line parallel to each of the vectors, forming a parallelogram.
3rd Add the axes and check that your result is the same as the vector you initially had.
Know more:
- Strength
- Acceleration
- Vector Quantities
Exercises
01-(PUC-RJ) The hour and minute hands of a Swiss watch are respectively 1 cm and 2 cm. Assuming that each clock hand is a vector that leaves the center of the clock and points toward the numbers at the end of the clock. clock, determine the vector resulting from the sum of the two vectors corresponding to the hour and minute hands when the clock reads 6 hours.
a) The vector has a 1 cm modulus and points in the direction of number 12 on the clock.
b) The vector has a module of 2 cm and points in the direction of number 12 on the clock.
c) The vector has a 1 cm modulus and points in the direction of number 6 on the clock.
d) The vector has a module of 2 cm and points in the direction of number 6 on the clock.
e) The vector has a module of 1.5 cm and points in the direction of number 6 on the clock.
a) The vector has a 1 cm modulus and points in the direction of number 12 on the clock.
02-(UFAL-AL) The location of a lake, in relation to a prehistoric cave, required walking 200 m in a certain direction and then 480 m in a direction perpendicular to the first. The distance in a straight line from the cave to the lake was, in meters,
a) 680
b) 600
c) 540
d) 520
e) 500
d) 520
03-(UDESC) A "freshman" from the Physics Course was tasked with measuring the displacement of an ant moving on a flat, vertical wall. The ant performs three successive displacements:
1) an offset of 20 cm in the vertical direction, wall below;
2) a displacement of 30 cm in the horizontal direction, to the right;
3) a displacement of 60 cm in the vertical direction, wall above.
At the end of the three displacements, we can say that the resulting displacement of the ant has a modulus equal to:
a) 110 cm
b) 50 cm
c) 160 cm
d) 10 cm
b) 50 cm
