11 exercises on matrix multiplication

Study with the 11 exercises on matrix multiplication, all with step-by-step resolution so you can solve your doubts and do well in exams and entrance exams.

question 1

Given the following matrices, check the option that indicates only possible products.

a) C.A, B.A, A.D.
b) D.B, D.C, A.D.
c) AC, D.A, C.D.
d) B.A, A.B, D.C
e) A.D., D.C., C.A.

See Answer

Correct answer: c) AC, D.A, C.D

A.C is possible because the number of columns in A (1) is equal to the number of rows in C (1).

D.A is possible, because the number of columns in D (2) is equal to the number of rows in A (2).

C.D is possible because the number of columns in C (3) is equal to the number of rows in D (3).

question 2

Make matrix product A. B.

See Answer

First we must check if it is possible to carry out the multiplication.

Since A is a 2x3 matrix and B a 3x2 matrix, it is possible to multiply, as the number of columns in A is equal to the number of rows in B.

We checked the dimensions of the matrix resulting from the multiplication.

Calling the result matrix of product A. B of matrix C, this will have two rows and two columns. Remember that the result matrix of the product "inherits" the number of rows from the first and the number of columns from the second.

Therefore, matrix C will be of type 2x2. Building the generic matrix C, we have:

C =

To calculate c11, we multiply the first line of A for the first column of B, adding the multiplied terms.

c11 = 3.1 + (-2).0 + 1.4 = 3 + 0 + 4 = 7

To calculate c12, we multiply the first line of A for the second column of B, adding the multiplied terms.

c12 = 3.3 + (-2).(-5) + 1.1 = 9 + 10 + 1 = 20

To calculate c21, we multiply the second line of A for the first column of B, adding the multiplied terms.

c21 = 1.1 + 5.0 + (-1).4 = 1 + 0 + (-4) = -3

To calculate c22, we multiply the second line of A for the second column of B, adding the multiplied terms.

c22 = 1.3 + 5.(-5) + (-1).1 = 3 + (-25) + (-1) = -23

Writing matrix C with its terms.

C =

question 3

Solve the matrix equation and determine the values ​​of x and y.

See Answer

We verified that it is possible to multiply the matrices before equality, as they are of type 2x2 and 2x1, that is, the number of columns in the first is equal to the number of rows in the second. The result is the 2x1 matrix on the right side of the equality.

We multiply row 1 of the first matrix by column 1 of the second matrix and equal to 3.

-1.x + 2.y = 3
-x + 2y = 3 (equation I)

We multiply row 2 of the first matrix by column 1 of the second matrix and equal to -4.

4.x + (-3).y = -4
4x - 3y = -4 (equation II)

We have two equations and two unknowns and we can solve a system to determine x and y.

Multiplying both sides of equation I by 4 and adding I + II, we have:

Substituting y in equation I and solving for x, we have:

So we have

question 4

Given the following linear system, associate a matrix equation.

See Answer

There are three equations and three unknowns.

To associate a matrix equation to the system, we must write three matrices: the coefficients, the unknowns and the independent terms.

Coefficients matrix

Unknown matrix

Matrix of independent terms

matrix equation

Matrix of coefficients. matrix of unknowns = matrix of independent terms

question 5

(UDESC 2019)

Given the matrices 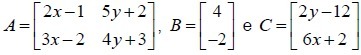and knowing that A. B = C, so the value of x + y is equal to:

a) 1/10
b) 33
c) 47
d) 1/20
e) 11

See Answer

Correct answer: c) 47

To determine the values ​​of x and y, we solve the matrix equation by obtaining a system. When solving the system, we get the values ​​of x and y.

Multiplying the matrices:

Isolating x in equation I

Substituting x in equation II

matching the denominators

To determine x, we substitute y into equation II

Thus,

x + y = 19 + 18
x + y = 47

question 6

(FGV 2016) Given the matrix 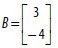and knowing that the matrix 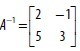is the inverse matrix of matrix A, we can conclude that the matrix X, which satisfies the matrix equation AX = B, has as the sum of its elements the number

a) 14
b) 13
c) 15
d) 12
e) 16

See Answer

Correct answer: b) 13

Any matrix multiplied by its inverse is equal to the identity matrix In.

Multiplying both sides of the equation AX = B by .

Making the product on the right side of the equation.

How the identity matrix is ​​the neutral element of the matrix product

Thus, the sum of its elements is:

10 + 3 = 13

question 7

Given the matrix following matrix A, calculate its inverse matrix, if any.

See Answer

A is invertible, or invertible if there is a square matrix of the same order which, when multiplying or being multiplied by A, results in the identity matrix.

We intend to identify the existence, or not, of a matrix for what:

Since A is a square matrix of order 2, must also have order 2.

Let's write the inverse matrix with its values ​​as unknowns.

Writing the matrix equation and solving the product.

Equating the equivalent terms on both sides of the equality.

3a + 7c = 1
5a + 12c = 0
3b + 7d = 0
5b + 12d = 1

We have a system with four equations and four unknowns. In this case, we can split the system into two. Each with two equations and two unknowns.

solving the system
Isolating a in the first equation

Substituting a in the second equation.

Replacing c

and the system:

Isolating b in the first equation

Substituting b in the second equation

Substituting d to determine b.

Replacing the determined values ​​in the inverse unknown matrix

Checking whether the calculated matrix is, in fact, the inverse matrix of A.

For this, we must perform the multiplications.

Therefore, fractions are invertible.

question 8

(EsPCEx 2020) Be the matrices . If AB=C, then x+y+z is equal to

a) -2.
b) -1.
c) 0.
d) 1.
e) 2.

See Answer

Correct answer: e) 2.

To determine the unknowns x, y and z, we must perform the matrix equation. As a result, we will have a linear system of three equations and three unknowns. When solving the system, we determine x, y, and z.

By the equality of matrices, we have:

Adding equations I and III

So x = -4/2 = -2

Substituting x = -2 in equation I and isolating z.

Substituting the values ​​of x and z in equation II.

Substituting the values ​​of x and y in equation I, we have:

Thus, we have to:

Therefore, the sum of the unknowns is equal to 2.

question 9

(PM-ES) About matrix multiplication, Fabiana wrote the following sentences in her notebook:

What Fabiana says is correct:

a) only in I.
b) only in II.
c) only in III.
d) only in I and III.
e) only in I and IV

See Answer

Correct answer: e) only in I and IV

It is only possible to multiply matrices when the number of columns in the first is equal to the number of rows in the second.

Therefore, sentence III is already discarded.

The matrix C, will have the number of rows of A and the number of columns of B.

Thus, sentences I and IV are correct.

question 10

Given matrix A, determine .

See Answer

Step 1: Determine .

Step 2: Determine the transposed matrix .

We obtain the transposed matrix of A by orderly swapping the rows for the columns.

Step 3: Solve the matrix product .

Therefore, the result of the matrix product is:

question 11

(UNICAMP 2018) The and B real numbers such that the matrix satisfies the equation , on what I is the order 2 identity matrix. Therefore, the product ab it's the same as

a) −2.
b) −1.
c) 1.
d) 2.

See Answer

Correct answer: a) -2.

Step 1: Determine .

Step 2: Determine a. THE.

Step 3: Determine b. I, where I is the identity matrix.

Step 4: Add aA + bI.

Step 5: Match the corresponding terms in.

Step 6: Solve the system by isolating a in equation I.

Substituting in equation II.

Replacing the value of b

Step 7: perform the multiplication a.b.

learn more about Matrix Multiplication.

You may be interested in:

Matrices - Exercises
Matrices
Matrices and Determinants
Types of Matrices