You decimal numbers they are non-integer rational numbers (Q) expressed by commas and which have decimal places, for example: 1.54; 4,6; 8.9, etc. They can be positive or negative.
Decimal places are counted from the comma, for example the number 12,451 has three decimal places, that is, three digits after the comma.
Integers
Unlike decimal numbers, whole numbers are real numbers (positive or negative) represented by the letter Z. They don't have a comma, for example: 1; 2; -3; -4, etc.
Fractional Numbers
Although they can have a corresponding value, fractional numbers are expressed as follows:
- ½ (one half) corresponding to the decimal 0.5
- ¾ (three quarters) which corresponds to the 0.75 decimal
- ¼ (one quarter) which corresponds to 0.25
Therefore, all decimal numbers can be expressed by fractions.
Reading Decimal Numbers: Examples
The reading of decimal numbers is done by joining the integer part of the number (expressed before the comma) and the number of decimal places (after the comma) which corresponds to the fractional part: tenth, hundredth, thousandth, tenth of a thousandth, hundredth of a thousandth, millionth, etc.
To better understand, see below some examples:
- 0.1: one tenth
- 0.4: four tenths
- 0.01: one hundredth
- 0.35: thirty-five hundredths
- 0.125: one hundred and twenty five thousandths
- 1.50: one integer and fifty hundredths
- 2.1: two integers and one tenth
- 4.8: four integers and eight tenths
Operations with Decimal Numbers: Addition, Subtraction, Multiplication and Division
To perform the decimal number operations, we must align the numbers according to the comma and the decimal places they have.
Addition
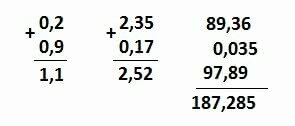
Subtraction
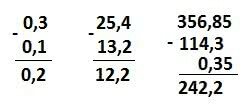
Multiplication
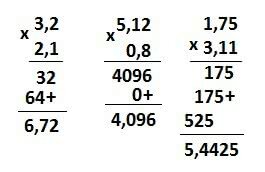
Division

Learn more about operations with decimal numbers.
Solved Exercises
1. Indicate which decimal numbers are expressed by the following fractions:
The) 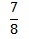
B) 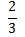
ç) 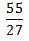
d) 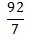
and) 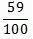
a) 0.875
b) 0.66
c) 2,037
d) 13.14
e) 0.59
2. Add up the decimal numbers below:
a) 0.34+057
b) 0.098+2.4
c) 7.9+8.56
d) 0.002+0.01
e) 97.9+52.54
a) 0.91
b) 2.498
c) 16.46
d) 0.012
e) 150.44
3. (Enem-2011) The owner of a mechanic shop needs a piston of the parts of an engine, 68 mm in diameter, to repair a car. To get one, this owner goes to a junkyard and there finds pistons with diameters equal to 68.21 mm; 68.102 mm; 68.001 mm; 68.02 mm and 68.012 mm.
To place the piston in the engine being repaired, the shop owner will have to purchase the one with the closest diameter to what he needs.
In this condition, the shop owner must buy the diameter piston
a) 68.21 mm.
b) 68.102 mm.
c) 68.02 mm.
d) 68.012 mm.
e) 68.001 mm.
Alternative e) 68.001 mm.
Learn more about numbers in articles:
- Decimal Numbering System
- real numbers
- Rational Numbers
- irrational numbers
- Natural Numbers
- multiplication tables
- Mathematical Symbols

