Potentiation: how to calculate, examples and exercises

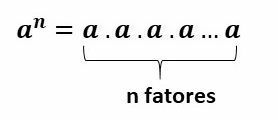
Power is a mathematical operation where a value called base is multiplied by itself the amount of times indicated by the exponent.

To calculate the power we do a multiplication of equal factors, where these factors are the basis of the power.

The number of times the base repeats is indicated by the exponent.

The terms of the potentiation are:

start style math size 18px base to power of exponent equals power end of style

Example 1
start style math size 18px 4 squared end style

THE base is the 4, is the factor that will be multiplied.
O exponent is the 2, is the number of times the 4 will be multiplied by itself.

Example 2
start style math size 18px 5 cubed end style

5 is the base and 3 is the exponent.

Thus, the 5 is the factor that will be repeated three times in the multiplication.

5 cubed equals 5 space. space 5 space. space 5 5 cubed equals 25 space. space 5 5 cubed equals 125

Example 3
start style math size 18px 2 to power of 4 end style

The base is 2, and the exponent is 4.

2 to the power of 4 equals 2 space. space 2 space. space 2 space. space 2 2 to the power of 4 equals 4 space. space 2 space. space 2 2 to the power of 4 equals 8 space. space 2 2 to the power of 4 equals 16

How to calculate the power of negative numbers

Negative based potentiation

To calculate powers with a negative base, simply repeat the base in the multiplication the number of times indicated by the exponent and identify the sign.

If the base is negative and the exponent is even, the result is positive.

Example
open parentheses minus 2 close parentheses squared equals open parentheses minus 2 close parentheses space. space opens parentheses minus 2 closes parentheses space equals space 4

Its base value is -2 (minus two) that is being raised to the exponent 2, so it is necessary to use parentheses.

instagram story viewer

If the base is negative and the exponent is odd, the result is negative.

Example

Power with negative exponent

To calculate a power with a negative exponent, the base is inverted and the exponent becomes positive. Then raise the numerator and denominator to the positive exponent.

It is important to remember that the reciprocal of a whole number is a fraction.

Example: integer base with negative exponent

$5 to the power of minus 2 end of exponential equals open parentheses 1 fifth closes parentheses squared equals 1 squared over 5 squared equals numerator 1 space. space 1 over denominator 5 space. space 5 end of fraction equals 1 over 25$

Example: fractional base with negative exponent

open parentheses 2 over 3 close parentheses to the power of minus 3 end of exponential equals open parentheses 3 over 2 close parentheses cubed equals 3 over 2.3 over 2.3 over 2 equals space 27 over 8

learn more about power with negative exponent.

How to calculate powers with fractional exponents

To calculate a power with a fractional exponent it is necessary to transform the power into a root.

The denominator of the exponent becomes the root index.
The numerator of the exponent is kept as the exponent of the base.
The base and the new exponent become the radicand of the root.

Example
start style math size 18px 4 to the power of 3 over 2 end of exponential end of style

The base is 4 and the exponent is 3/2.

The denominator 2 of the exponent becomes the fraction index. So it's going to be a square root.
The numerator 3 of the exponent is kept as the exponent of base 4.