THE second degree equation gets its name because it is a polynomial equation whose highest degree term is squared. Also called a quadratic equation, it is represented by:
ax2 + bx + c = 0
In a 2nd degree equation, the x is the unknown and represents an unknown value. already the lyrics The, B and ç are called equation coefficients.
The coefficients are real numbers and the coefficient The it has to be different from zero, otherwise it becomes a 1st degree equation.
Solving a second degree equation means looking for real values of x, which make the equation true. These values are called the roots of the equation.
A quadratic equation has at most two real roots.
Complete and Incomplete High School Equations
2nd degree equations complete are those that have all the coefficients, that is, a, b and c are different from zero (a, b, c ≠ 0).
For example, the 5x equation2 + 2x + 2 = 0 is complete, as all coefficients are non-zero (a = 5, b = 2 and c = 2).
A quadratic equation is incomplete when b = 0 or c = 0 or b = c = 0. For example, the 2x equation
2 = 0 is incomplete because a = 2, b = 0 and c = 0Solved Exercises
1) Determine the values of x that make the equation 4x2 - 16 = 0 true.
Solution:
The given equation is an incomplete 2nd degree equation, with b = 0. For equations of this type, we can solve by isolating the x. Thus:
Note that the square root of 4 can be 2 and - 2, as these two squared numbers result in 4.
So the roots of the 4x equation2 - 16 = 0 are x = - 2 and x = 2
2) Find the value of x so that the area of the rectangle below is equal to 2.
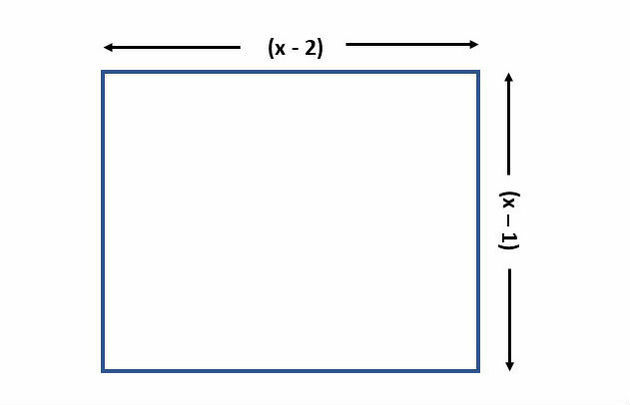
Solution:
The area of the rectangle is found by multiplying the base by the height. So, we must multiply the given values and equal to 2.
(x - 2). (x - 1) = 2
Now let's multiply all terms:
x. x - 1. x - 2. x - 2. (- 1) = 2
x2 - 1x - 2x + 2 = 2
x2 - 3x + 2 - 2 = 0
x2 - 3x = 0
After solving the multiplications and simplifications, we find an incomplete quadratic equation, with c = 0.
This type of equation can be solved through the factorization, because the x is repeated in both terms. So we're going to put it in evidence.
x. (x - 3) = 0
For the product to be equal to zero, either x = 0 or (x - 3) = 0. However, replacing x by zero, the measurements of the sides are negative, so this value will not be the answer to the question.
So we have that the only possible result is (x - 3) = 0. Solving this equation:
x - 3 = 0
x = 3
In this way, the value of the x so that the area of the rectangle is equal to 2 is x = 3.
Bhaskara formula
When a quadratic equation is complete, we use the Bhaskara formula to find the roots of the equation.
The formula is presented below:
Delta formula
In Bhaskara's formula, the Greek letter appears Δ (delta), which is called the equation's discriminant, because according to its value it is possible to know the number of roots the equation will have.
To calculate the delta we use the following formula:
Step by step
To solve a 2nd degree equation, using Bhaskara's formula, we must follow these steps:
1st step: Identify the coefficients The, B and ç.
The terms of the equation do not always appear in the same order, so it is important to know how to identify the coefficients, regardless of the sequence in which they are.
the coefficient The is the number that goes with the x2, O B is the number that accompanies the x it's the ç is the independent term, that is, the number that appears without the x.
2nd Step: Calculate the delta.
To calculate the roots it is necessary to know the value of the delta. To do this, we replace the letters in the formula with the coefficient values.
We can, from the delta value, know in advance the number of roots that the 2nd degree equation will have. That is, if the value of Δ is greater than zero (Δ > 0), the equation will have two real and distinct roots.
If on the contrary, delta is less than zero (Δ ), the equation will not have real roots and if it is equal to zero (Δ = 0), the equation will have only one root.
3rd Step: Calculate the roots.
If the value found for delta is negative, you don't need to do any more calculations and the answer is that the equation has no real roots.
If the delta value is equal to or greater than zero, we must replace all letters by their values in Bhaskara's formula and calculate the roots.

Exercise solved
Determine the roots of the 2x equation2 - 3x - 5 = 0
Solution:
To solve this, we must first identify the coefficients, so we have:
a = 2
b = - 3
c = - 5
Now we can find the delta value. We must be careful with the rules of signs and remember that we must solve potentiation and multiplication first, and then addition and subtraction.
Δ = (- 3)2 - 4. (- 5). 2 = 9 +40 = 49
As the value found is positive, we will find two distinct values for the roots. So, we must solve Bhaskara's formula twice. So we have:
So the roots of the 2x equation2 - 3x - 5 = 0 are x = 5/2 and x = - 1.
2nd Degree Equation System
When we want to find values of two different unknowns that simultaneously satisfy two equations, we have a system of equations.
The equations that make up the system can be of the 1st degree and the 2nd degree. To solve this kind of system we can use the substitution method and the addition method.
Exercise solved
Solve the system below:
Solution:
To solve the system, we can use the addition method. In this method, we add similar terms from the 1st equation with those from the 2nd equation. Thus, we reduce the system to a single equation.
We can still simplify all the terms in the equation by 3 and the result will be the equation x2 - 2x - 3 = 0. Solving the equation, we have:
Δ = 4 - 4. 1. (- 3) = 4 + 12 = 16
After finding the x-values, we must not forget that we still have to find the y-values that make the system true.
To do this, just replace the values found for x in one of the equations.
y1 - 6. 3 = 4
y1 = 4 + 18
y1 = 22
y2 - 6. (-1) = 4
y2 + 6 = 4
y2 = - 2
Therefore, the values that satisfy the proposed system are (3, 22) and (-1, - 2)
You may also be interested in First Degree Equation.
Exercises
question 1
Solve the complete quadratic equation using Bhaskara's Formula:
2x2 + 7x + 5 = 0
First of all it is important to observe each coefficient in the equation, therefore:
a = 2
b = 7
c = 5
Through the formula of the discriminant of the equation, we must find the value of Δ.
This is to later find the roots of the equation through the general formula or Bhaskara's formula:
Δ = 72 – 4. 2. 5
Δ = 49 - 40
Δ = 9
Note that if the value of Δ is greater than zero (Δ > 0), the equation will have two real and distinct roots.
So, after finding the Δ, let's replace it in Bhaskara's formula:
Therefore, the values of the two real roots are: x1 = - 1 and x2 = - 5/2
Check out more questions at High School Equation - Exercises
question 2
Solve the incomplete second degree equations:
a) 5x2 – x = 0
First, we look for the coefficients of the equation:
a=5
b= - 1
c = 0
It is an incomplete equation where c = 0.
To calculate it we can use factorization, which in this case is putting x in evidence.
5x2 – x = 0
x. (5x-1) = 0
In this situation, the product will be equal to zero when x = 0 or when 5x -1 = 0. So let's calculate the value of x:
So the roots of the equation are x1 = 0 and x2 = 1/5.
b) 2x2 – 2 = 0
a = 2
b = 0
c = - 2
It is an incomplete second degree equation, where b = 0, its calculation can be done by isolating the x:
x1 = 1 and x2 = - 1
So the two roots of the equation are x1 = 1 and x2 = - 1
c) 5x2 = 0
a = 5
b = 0
c = 0
In this case, the incomplete equation presents coefficients b and c equal to zero (b = c = 0):
Therefore, the roots of this equation have the values x1 = x2 = 0
To learn more, read also:
- Quadratic Function
- Sum and Product
- inequality
- irrational equations
- Vertex of the Parabola