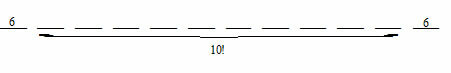In the construction of roads and railways, the use of trigonometry is essential, especially in situations involving changes in directions. Curves are designed based on circumference arc models and the center angle measurement (relative to the curve). We are going through some examples to demonstrate the calculation performed in order to determine the length of the curve.
Example 1
A road design demonstrates a curve shaped like an arc of a circumference with a radius measuring 200 meters. From point A (beginning of the curve) to point B (end of the curve) the road changed its direction by 40º. How long will the curve be?

Considering that the complete turn around the circle is equivalent to 360º and in matters of length a C = 2 * π * r, we can adopt a rule of three relating the known measures. Watch: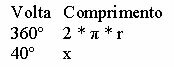
360x = 40 * 2 * 3.14 * 200
360x = 50240
x = 50 240 / 360
x = 139.5 (approximately)
The length of the curve will be approximately 139.5 meters.
In civil engineering, very tall buildings, considered to be skyscrapers, are designed to suffer small oscillations, due to the force imposed by the winds, because the higher, the greater the speed of the wind.
Example 2
A 400 meter building has an oscillation of 0.3º. Determine the length of the arc relative to this oscillation?

360x = 0.3 * 2 * 3.14 * 400
360x = 753.6
x = 753.6 / 360
x = 2.1 m (approximately)
Do not stop now... There's more after the advertising ;)
by Mark Noah
Graduated in Mathematics
Brazil School Team
Trigonometry - Math - Brazil School
Would you like to reference this text in a school or academic work? Look:
SILVA, Marcos Noé Pedro da. "Length of a Curve"; Brazil School. Available in: https://brasilescola.uol.com.br/matematica/comprimento-uma-curva.htm. Accessed on June 27, 2021.