simple interest it is an addition calculated on the initial value of a financial investment or a purchase made on credit, for example.
The initial amount of a debt, loan or investment is called equity. This amount is subject to a correction, called the interest rate, which is expressed as a percentage.
Interest is calculated considering the period of time the capital was invested or borrowed.
Example
A customer of a store wants to buy a television, which costs 1000 reais in cash, in 5 equal installments. Knowing that the store charges an interest rate of 6% per month on installment purchases, what is the value of each installment and the total amount the customer will pay?
When we buy something in installments, interest determines the final amount we will pay. Thus, if we buy a television on installment, we will pay an amount corrected by the fee charged.
By paying this amount in five months, if there were no interest, we would pay 200 reais per month (1000 divided by 5). But 6% was added to this value, so we have:
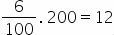
In this way, we will have an increase of R$12 per month, that is, each installment will be R$212. This means that, in the end, we will pay R$60 more than the initial amount.
Therefore, the total value of the installment television is R$1060.
Formula: How to Calculate Simple Interest?
The formula for calculating simple interest is expressed by:
J = C. i. t
Where,
J: fees
Ç: capital
i: interest rate. To substitute in the formula, the rate must be written as a decimal number. To do this, just divide the given value by 100.
t: time. The interest rate and time must refer to the same time unit.
We can also calculate the amount, which is the total amount received or due, at the end of the time period. This amount is the sum of interest with the initial amount (capital).
Your formula will be:
M = C + J → M = C + C. i. t
From the above equation, therefore, we have the expression:
M = C. (1 + i. t)
Examples
1) How much did the amount of R$ 1200, applied at simple interest, at the rate of 2% per month, at the end of 1 year and 3 months?
Being:
C = 1200
i = 2% per month = 0.02
t = 1 year and 3 months = 15 months (you have to transform into months to stay in the same unit of time as the interest rate.
J = C. i. t = 1200. 0,02. 15 = 360
Thus, the yield at the end of the period will be BRL 360.
2) A principal of R$400, applied to simple interest at a rate of 4% per month, resulted in the amount of R$480 after a certain period of time. What was the application time?
Considering,
C = 400
i = 4% per month = 0.04
M = 480
we have:
Compound interest
There is yet another form of financial correction called compound interest. This type of correction is most often used in business and financial transactions.
Unlike simple interest, compound interest is applied to interest on interest. Thus, the compound interest system is called "accumulated capitalization".
Remember that in calculating simple interest, the interest rate is calculated on the same amount (capital). This is not the case with compound interest, as in this case the amount applied changes each period.
Read too:
- Simple Interest Exercises
- Compound Interest Exercises
- Simple and Compound Interest
- Financial math
- Percentage
- Percentage Exercises
- Arithmetic average
- Combinatorial Analysis
- Ratio and Proportion
- Math Formulas
Solved Exercises
To better understand the application of the simple interest concept, let's see below two solved exercises, one of which fell on Enem in 2011.
1) Lúcia lent 500 reais to her friend Márcia at a rate of 4% per month, who, in turn, agreed to pay the debt within a period of 3 months. Calculate the amount that Márcia will pay Lucia in the end.
First we have to transform the interest rate to decimal number, dividing the given value by 100. Then we will calculate the amount of the interest rate on (principal) capital during the 1 month period:
Soon:
J = 0.04. 500 = 20
Therefore, the amount of interest in 1 month will be R$20.
If Márcia paid her debt in 3 months, just calculate the amount of interest for 1 month for the period, that is, R$20. 3 months = R$60. In total, she will pay an amount of R$560.
Another way to calculate the total amount that Márcia will pay her friend is to apply the amount formula (sum of interest to principal amount):
Soon,
M = C. (1 + i. t)
M = 500. (1 + 0,04. 3)
M = 500. 1,12
M = R$560
2) Enem-2011
A young investor needs to choose which investment will bring him the greatest financial return in an investment of R$500.00. To do this, it researches the income and tax to be paid on two investments: savings and CDB (bank deposit certificate). The information obtained is summarized in the table:
| Monthly income (%) | IR (income tax) | |
| Savings | 0,560 | free |
| CBD | 0,876 | 4% (on the gain) |
For the young investor, at the end of a month, the most advantageous application is:
a) savings, as it will total an amount of BRL 502.80
b) savings, as it will total an amount of BRL 500.56
c) the CDB, as it will total an amount of BRL 504.38
d) the CDB, as it will total an amount of BRL 504.21
e) the CDB, as it will total an amount of BRL 500.87
In order to know which of the alternatives is more advantageous for the young investor, we must calculate the return he will have in both cases:
Savings:
Application: BRL 500
Monthly Yield (%): 0.56
Income Tax Exempt
Soon,
First divide the rate by 100, to transform it into a decimal number, then apply to capital:
0,0056 * 500 = 2,8
Therefore, the gain in savings will be 2.8 + 500 = BRL 502.80
CDB (bank deposit certificate)
Application: BRL 500
Monthly Income (%): 0.876
Income Tax: 4% on the gain
Soon,
Transforming the rate from to decimal we find 0.00876, applying to capital:
0,00876 * 500= 4,38
Therefore, the gain in the CDB will be 4.38 + 500 = R$504.38
However, we must not forget to apply the income tax rate (IR) on the value found:
4% of 4.38
0,04 * 4,38= 0,1752
To find the final value, we subtract this value from the gain above:
4,38 - 0,1752 = 4,2048
Therefore, the final balance of the CDB will be R$504.2048 which is approximately R$504.21
Alternative d: the CDB, as it will total an amount of BRL 504.21
See too: how to calculate percentage?