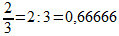You numerical sets they bring together several sets whose elements are numbers. They are formed by natural, integer, rational, irrational and real numbers. The branch of mathematics that studies numerical sets is set theory.
Check below the characteristics of each one of them, such as concept, symbol and subsets.
Set of Natural Numbers (N)
The set of natural numbers is represented by N. It gathers the numbers we use to count (including zero) and is infinite.
Subsets of Natural Numbers
- N* = {1, 2, 3, 4, 5..., n, ...} or N* = N – {0}: sets of non-zero natural numbers, that is, without zero.
- NP = {0, 2, 4, 6, 8..., 2n, ...}, where n ∈ N: set of even natural numbers.
- Ni = {1, 3, 5, 7, 9..., 2n+1, ...}, where n ∈ N: set of odd natural numbers.
- P = {2, 3, 5, 7, 11, 13, ...}: set of prime natural numbers.
Set of Integers (Z)
The set of whole numbers is represented by Z. It brings together all the elements of the natural numbers (N) and their opposites. Thus, it is concluded that N is a subset of Z (N ⊂ Z):
Subsets of Integers
- Z* = {..., –4, –3, –2, –1, 1, 2, 3, 4, ...} or Z* = Z – {0}: sets of non-zero integers, ie, without the zero.
- Z+ = {0, 1, 2, 3, 4, 5, ...}: set of integer and non-negative numbers. Note that Z+ = No.
- Z*+= {1, 2, 3, 4, 5, ...}: set of positive integers without the zero.
- Z – = {..., –5, –4, –3, –2, –1, 0}: set of non-positive integers.
- Z*–= {..., –5, –4, –3, –2, –1}: set of negative integers without zero.
Set of Rational Numbers (Q)
The set of rational numbers is represented by Q. Gathers all numbers that can be written in the form p/q, being P and what integers and q≠0.
Q = {0, ±1, ±1/2, ±1/3,..., ±2, ±2/3, ±2/5,..., ±3, ±3/2, ±3/ 4, ...}
Note that every whole number is also a rational number. So Z is a subset of Q.
Subsets of Rational Numbers
- Q* = subset of the non-zero rational numbers, formed by the rational numbers without the zero.
- Q+ = subset of non-negative rational numbers, formed by positive rational numbers and zero.
- Q*+ = subset of the positive rational numbers, formed by the positive rational numbers, without the zero.
- Q– = subset of non-positive rational numbers, formed by negative rational numbers and zero.
- Q*– = subset of negative rational numbers, formed negative rational numbers, without zero.
Set of Irrational Numbers (I)
The set of irrational numbers is represented by I. Gathers inexact decimal numbers with an infinite, non-periodic representation, for example: 3.141592... or 1.203040...
It is important to note that the periodic tithes they are rational and not irrational numbers. They are decimal numbers that repeat after the comma, for example: 1.3333333...
Set of Real Numbers (R)
The set of real numbers is represented by R. This set is formed by the rational (Q) and irrational (I) numbers. Thus, we have that R = Q ∪ I. Furthermore, N, Z, Q and I are subsets of R.
But note that if a real number is rational, it cannot be irrational either. Likewise, if he is irrational, he is not rational.
Subsets of Real Numbers
- R*= {x ∈ R│x ≠ 0}: set of non-zero real numbers.
- R+= {x ∈ R│x ≥ 0}: set of non-negative real numbers.
- R*+= {x ∈ R│x > 0}: set of positive real numbers.
- R– = {x ∈ R│x ≤ 0}: set of non-positive real numbers.
- R*– = {x ∈ R│x
Also read about Numbers: what they are, history and sets.
Numerical Ranges
There is even a subset related to real numbers that are called intervals. be The and B real numbers and at real intervals:
extreme open range: ]a, b[ = {x ∈ R│a

Closed range of extremes: [a, b] = {x ∈ R│a ≤ x ≤ b}

Open range to the right (or left closed) of extremes: [a, b[ = {x ∈ R│a ≤ x

left open range (or closed to the right) of extremes: ]a, b] = {x ∈ R│a

Properties of Numerical Sets
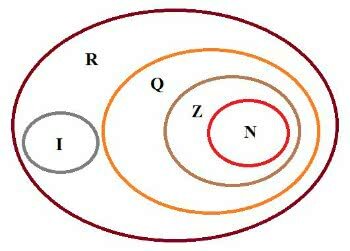
Diagram of numerical sets
To facilitate studies on numerical sets, below are some of their properties:
- The set of natural numbers (N) is a subset of the integers: Z (N ⊂ Z).
- The set of integers (Z) is a subset of the rational numbers: (Z ⊂ Q).
- The set of rational numbers (Q) is a subset of the real numbers (R).
- The sets of natural (N), integers (Z), rational (Q) and irrational (I) numbers are subsets of the real numbers (R).
Entrance Exam Exercises with Feedback
1. (UFOP-MG) Regarding the numbers a = 0.49999... and b = 0.5, it is correct to state:
a) b = a + 0.011111
b) a = b
ç) The is irrational and B it's rational
gives
Alternative b: a = b
2. (UEL-PR) Note the following numbers:
I. 2,212121...
II. 3,212223...
III. π/5
IV. 3,1416
V. √– 4
Check the alternative that identifies the irrational numbers:
a) I and II.
b) I and IV.
c) II and III.
d) II and V.
e) III and V.
Alternative c: II and III.
3. (Cefet-CE) The set is unitary:
a) {x ∈ Z│x b) {x ∈ Z│x2 > 0}
c) {x ∈ R│x2 = 1}
d) {x ∈ Q│x2
e) {x ∈ N│1
Alternative e: {x ∈ N│1
Read too:
- Set theory
- Complex numbers
- Operations with Sets
- Exercises on Sets
- Numerical Set Exercises
- Exercises on Complex Numbers